Chainer at a Glance¶
Welcome to Chainer!
Chainer is a rapidly growing neural network platform. The strengths of Chainer are:
Python-based – Chainer is developed in Python, allowing for inspection and customization of all code in python and understandable python messages at run time
Define by Run – neural networks definitions are defined on-the-fly at run time, allowing for dynamic network changes
NumPy based syntax for working with arrays, thanks to CuPy implementation
Fully customizable – since Chainer is pure python, all classes and methods can be adapted to allow for the latest cutting edge or specialized approaches
Broad and deep support – Chainer is actively used for most of the current approaches for neural nets (CNN, RNN, RL, etc.), aggressively adds new approaches as they’re developed, and provides support for many kinds of hardware as well as parallelization for multiple GPUs
Mushrooms – tasty or deathly?¶
Let’s take a look at a basic program of Chainer to see how it works. For a dataset, we’ll work with Kaggle’s edible vs. poisonous mushroom dataset, which has over 8,000 examples of mushrooms, labelled by 22 categories including odor, cap color, habitat, etc., in a mushrooms.csv file.
How will Chainer learn which mushrooms are edible and which mushrooms will kill you? Let’s see!
The code below is from the glance example in the examples/glance directory.
Code Breakdown¶
Initialization¶
Let’s start the program. Here are the typical imports for a Chainer program. chainer.links contain trainable parameters and chainer.functions do not.
6 7 8 9 10 11 12 13 | import chainer as ch
from chainer import datasets
import chainer.functions as F
import chainer.links as L
from chainer import training
from chainer.training import extensions
import numpy as np
|
We’ll use Matplotlib for the graphs to show training progress.
15 16 | import matplotlib
matplotlib.use('Agg')
|
Trainer Structure¶
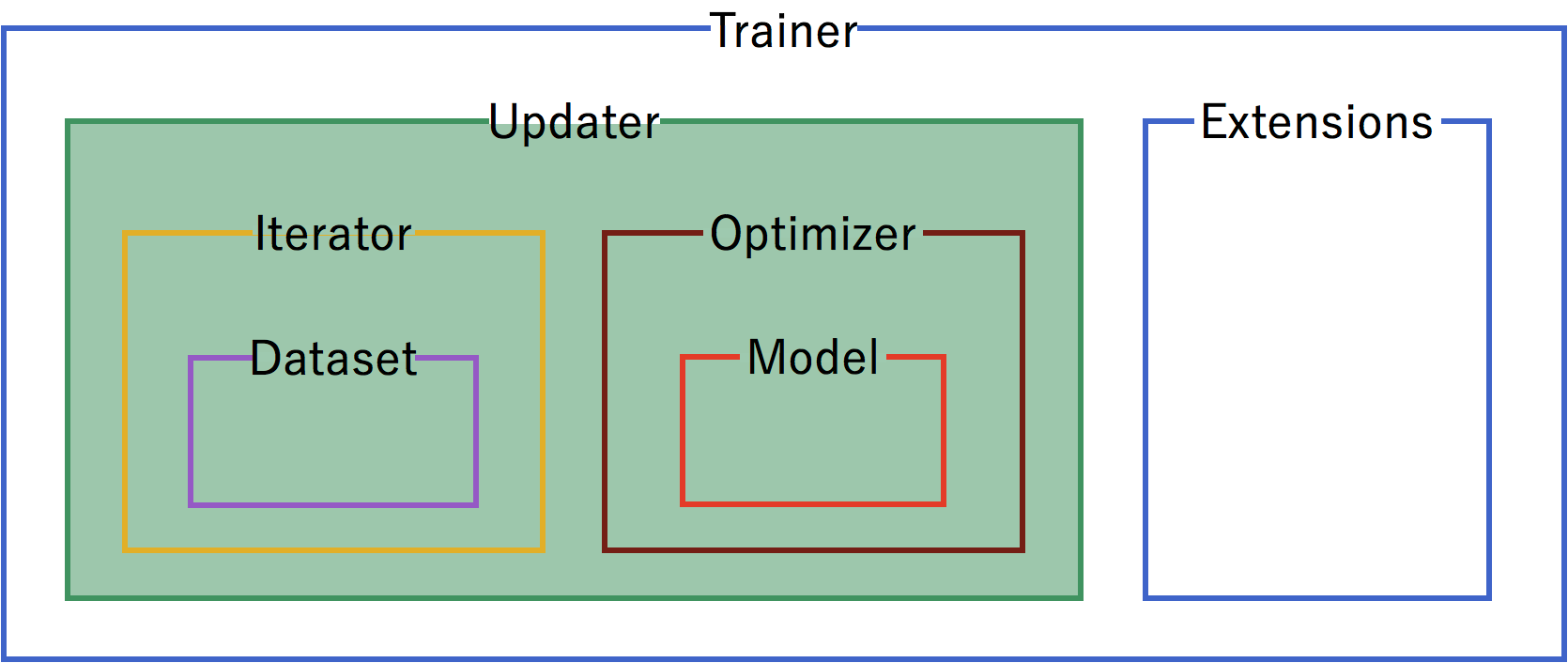
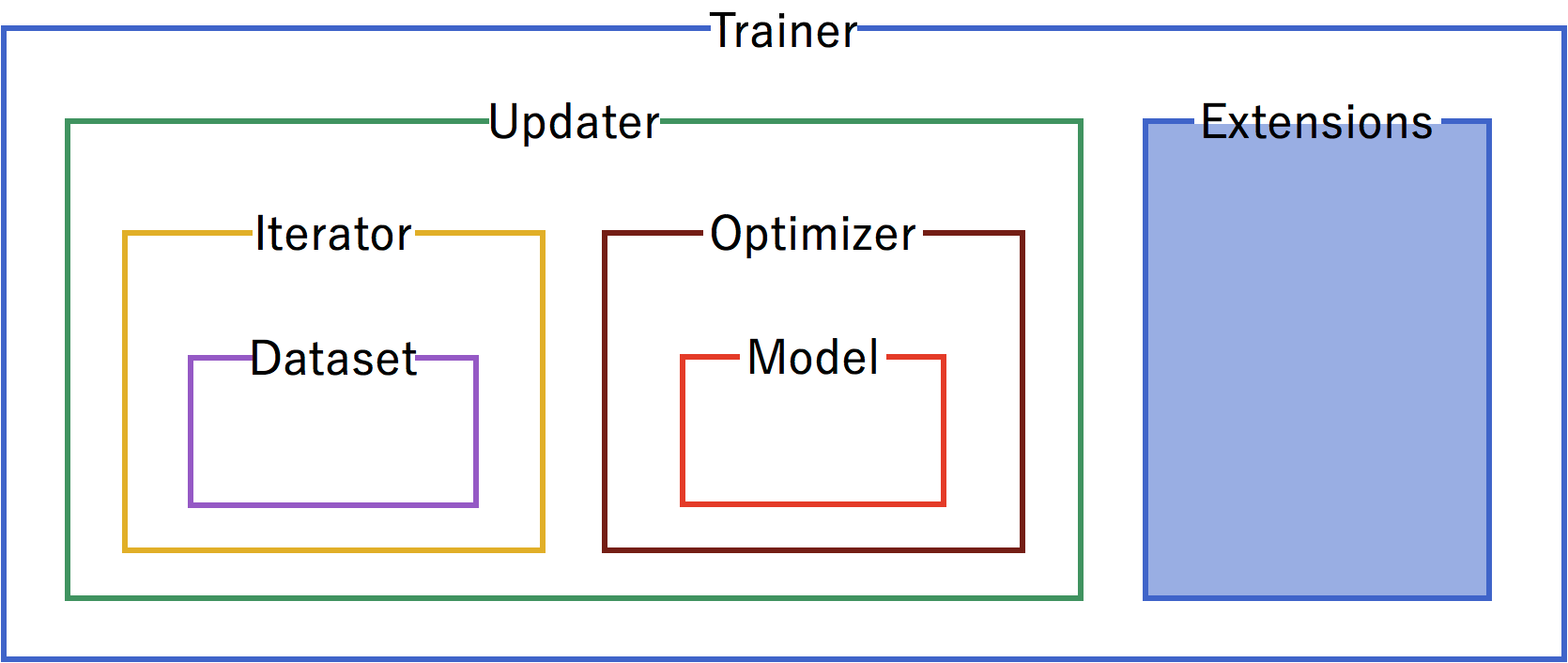
A trainer is used to set up our neural network and data for training. The components of the trainer are generally hierarchical, and are organized as follows:
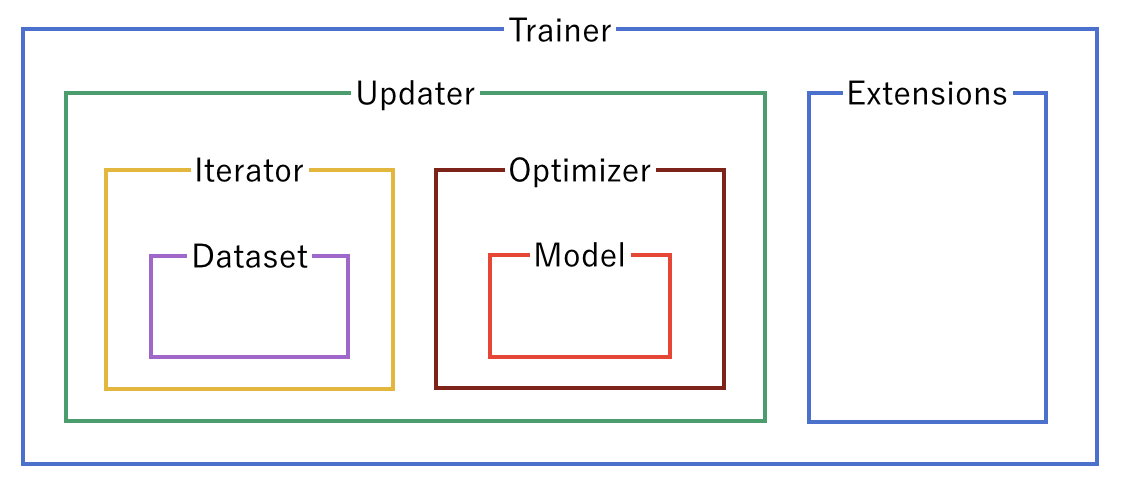
Each of the components is fed information from the components within it. Setting up the trainer starts at the inner components, and moves outward, with the exception of extensions, which are added after the trainer is defined.
Dataset¶
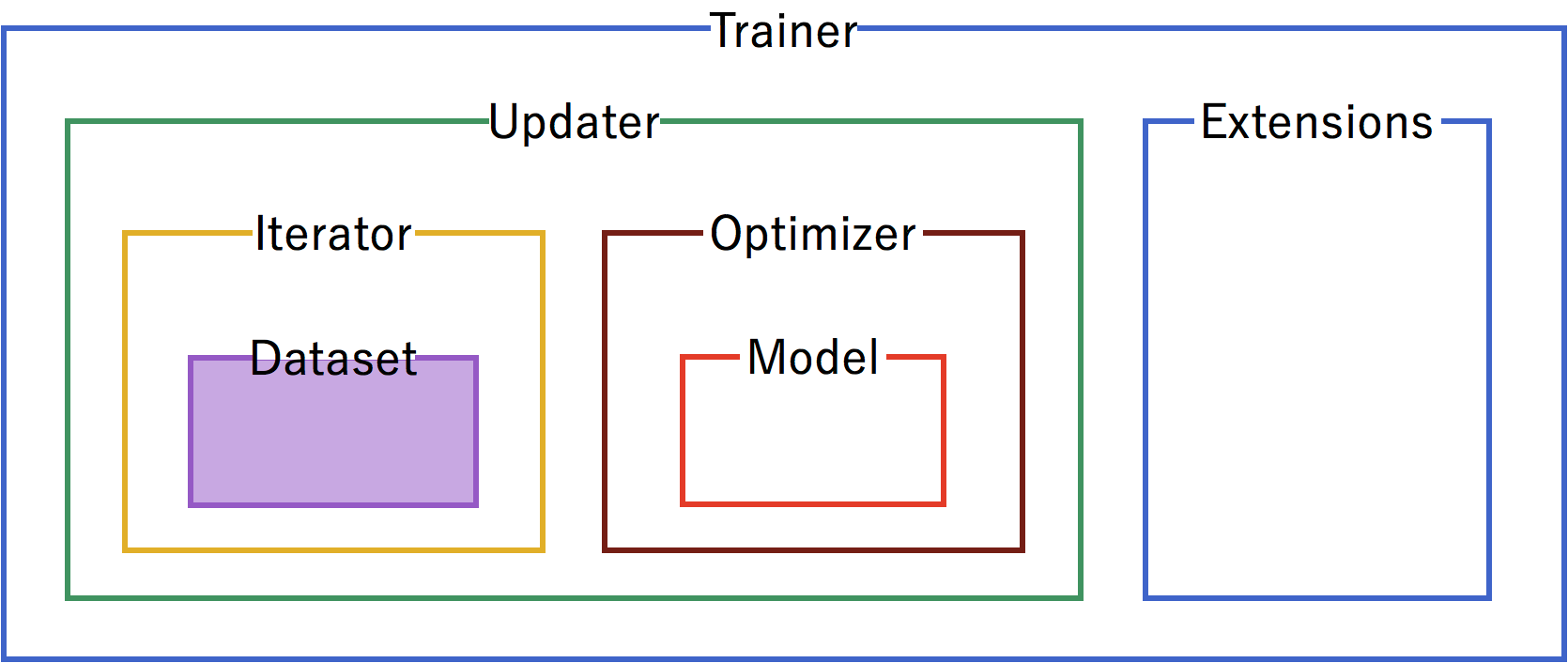
Our first step is to format the dataset. From the raw mushrooms.csv, we format the data into a Chainer TupleDataset.
18 19 20 21 22 23 24 25 26 27 | mushroomsfile = 'mushrooms.csv'
data_array = np.genfromtxt(
mushroomsfile, delimiter=',', dtype=str, skip_header=1)
for col in range(data_array.shape[1]):
data_array[:, col] = np.unique(data_array[:, col], return_inverse=True)[1]
X = data_array[:, 1:].astype(np.float32)
Y = data_array[:, 0].astype(np.int32)[:, None]
train, test = datasets.split_dataset_random(
datasets.TupleDataset(X, Y), int(data_array.shape[0] * .7))
|
Iterator¶

Configure iterators to step through batches of the data for training and for testing validation. In this case, we’ll use a batch size of 100. For the training iterator, repeating and shuffling are implicitly enabled, while they are explicitly disabled for the testing iterator.
29 30 31 | train_iter = ch.iterators.SerialIterator(train, 100)
test_iter = ch.iterators.SerialIterator(
test, 100, repeat=False, shuffle=False)
|
Model¶

Next, we need to define the neural network for inclusion in our model. For our mushrooms, we’ll chain together two fully-connected, Linear, hidden layers between the input and output layers.
As an activation function, we’ll use standard Rectified Linear Units (relu()).
Using the Sequential allows us to define the neural network model in a compact format.
34 35 36 37 38 39 40 | # Network definition
def MLP(n_units, n_out):
layer = ch.Sequential(L.Linear(n_units), F.relu)
model = layer.repeat(2)
model.append(L.Linear(n_out))
return model
|
Since mushrooms are either edible or poisonous (no information on psychedelic effects!) in the dataset, we’ll use a Link Classifier for the output, with 44 units (double the features of the data) in the hidden layers and a single edible/poisonous category for classification.
43 44 | model = L.Classifier(
MLP(44, 1), lossfun=F.sigmoid_cross_entropy, accfun=F.binary_accuracy)
|
Optimizer¶
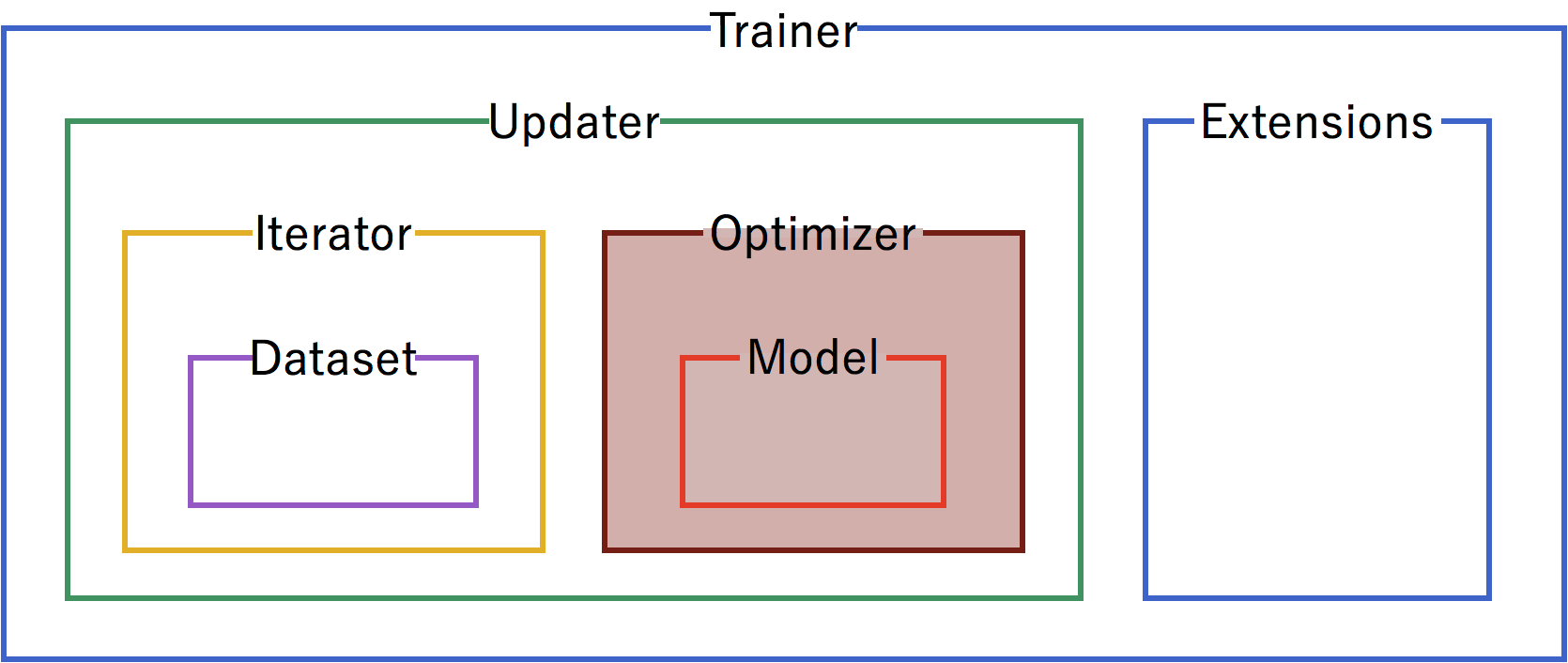
Pick an optimizer, and set up the model to use it.
46 47 | # Setup an optimizer
optimizer = ch.optimizers.SGD().setup(model)
|
Updater¶
Now that we have the training iterator and optimizer set up, we link them both together into the updater. The updater uses the minibatches from the iterator, and then does the forward and backward processing of the model, and updates the parameters of the model according to the optimizer. Setting the device=-1 sets the device as the CPU. To use a GPU, set device equal to the number of the GPU, usually device=0.
49 50 | # Create the updater, using the optimizer
updater = training.StandardUpdater(train_iter, optimizer, device=-1)
|
Set up the updater to be called after the training batches and set the number of batches per epoch to 100. The learning rate per epoch will be output to the directory result.
52 53 | # Set up a trainer
trainer = training.Trainer(updater, (50, 'epoch'), out='result')
|
Extensions¶
Use the testing iterator defined above for an Evaluator extension to the trainer to provide test scores.
If using a GPU instead of the CPU, set device to the ID of the GPU, usually 0.
54 55 | # Evaluate the model with the test dataset for each epoch
trainer.extend(extensions.Evaluator(test_iter, model, device=-1))
|
Save a computational graph from loss variable at the first iteration. main refers to the target link of the main optimizer. The graph is saved in the Graphviz’s dot format. The output location (directory) to save the graph is set by the out argument of trainer.
57 58 59 | # Dump a computational graph from 'loss' variable at the first iteration
# The "main" refers to the target link of the "main" optimizer.
trainer.extend(extensions.dump_graph('main/loss'))
|
Take a snapshot of the trainer object every 20 epochs.
61 | trainer.extend(extensions.snapshot(), trigger=(20, 'epoch'))
|
Write a log of evaluation statistics for each epoch.
63 64 | # Write a log of evaluation statistics for each epoch
trainer.extend(extensions.LogReport())
|
Save two plot images to the result directory.
66 67 68 69 70 71 72 73 74 | # Save two plot images to the result dir
if extensions.PlotReport.available():
trainer.extend(
extensions.PlotReport(['main/loss', 'validation/main/loss'],
'epoch', file_name='loss.png'))
trainer.extend(
extensions.PlotReport(
['main/accuracy', 'validation/main/accuracy'],
'epoch', file_name='accuracy.png'))
|
Print selected entries of the log to standard output.
76 77 78 79 | # Print selected entries of the log to stdout
trainer.extend(extensions.PrintReport(
['epoch', 'main/loss', 'validation/main/loss',
'main/accuracy', 'validation/main/accuracy', 'elapsed_time']))
|
Run the training.
81 82 | # Run the training
trainer.run()
|
Inference¶
Once the training is complete, only the model is necessary to make predictions. Let’s check that a random line from the test data set and see if the inference is correct:
84 85 86 87 88 89 90 91 92 | x, t = test[np.random.randint(len(test))]
predict = model.predictor(x[None]).data
predict = predict[0][0]
if predict >= 0:
print('Predicted Poisonous, Actual ' + ['Edible', 'Poisonous'][t[0]])
else:
print('Predicted Edible, Actual ' + ['Edible', 'Poisonous'][t[0]])
|
Output¶
Output for this instance will look like:
epoch main/loss validation/main/loss main/accuracy validation/main/accuracy elapsed_time
1 0.550724 0.502818 0.733509 0.752821 0.215426
2 0.454206 0.446234 0.805439 0.786926 0.902108
3 0.402783 0.395893 0.838421 0.835979 1.50414
4 0.362979 0.359988 0.862807 0.852632 2.24171
5 0.32713 0.329881 0.88 0.874232 2.83247
6 0.303469 0.31104 0.892456 0.887284 3.45173
7 0.284755 0.288553 0.901754 0.903284 3.9877
8 0.26801 0.272033 0.9125 0.907137 4.54794
9 0.25669 0.261355 0.920175 0.917937 5.21672
10 0.241789 0.251821 0.927193 0.917937 5.79541
11 0.232291 0.238022 0.93 0.925389 6.3055
12 0.222805 0.22895 0.934035 0.923389 6.87083
13 0.21276 0.219291 0.93614 0.928189 7.54113
14 0.204822 0.220736 0.938596 0.922589 8.12495
15 0.197671 0.207017 0.938393 0.936042 8.69219
16 0.190285 0.199129 0.941053 0.934842 9.24302
17 0.182827 0.193303 0.944386 0.942695 9.80991
18 0.176776 0.194284 0.94614 0.934042 10.3603
19 0.16964 0.177684 0.945789 0.945242 10.8531
20 0.164831 0.171988 0.949825 0.947347 11.3876
21 0.158394 0.167459 0.952982 0.949747 11.9866
22 0.153353 0.161774 0.956964 0.949347 12.6433
23 0.148209 0.156644 0.957368 0.951747 13.3825
24 0.144814 0.15322 0.957018 0.955495 13.962
25 0.138782 0.148277 0.958947 0.954147 14.6
26 0.135333 0.145225 0.961228 0.956695 15.2284
27 0.129593 0.141141 0.964561 0.958295 15.7413
28 0.128265 0.136866 0.962632 0.960547 16.2711
29 0.123848 0.133444 0.966071 0.961347 16.7772
30 0.119687 0.129579 0.967193 0.964547 17.3311
31 0.115857 0.126606 0.968596 0.966547 17.8252
32 0.113911 0.124272 0.968772 0.962547 18.3121
33 0.111502 0.122548 0.968596 0.965095 18.8973
34 0.107427 0.116724 0.970526 0.969747 19.4723
35 0.104536 0.114517 0.970877 0.969095 20.0804
36 0.099408 0.112128 0.971786 0.970547 20.6509
37 0.0972982 0.107618 0.973158 0.970947 21.2467
38 0.0927064 0.104918 0.973158 0.969347 21.7978
39 0.0904702 0.101141 0.973333 0.969747 22.3328
40 0.0860733 0.0984015 0.975263 0.971747 22.8447
41 0.0829282 0.0942095 0.977544 0.974947 23.5113
42 0.082219 0.0947418 0.975965 0.969347 24.0427
43 0.0773362 0.0906804 0.977857 0.977747 24.5252
44 0.0751769 0.0886449 0.977895 0.972147 25.1722
45 0.072056 0.0916797 0.978246 0.977495 26.0778
46 0.0708111 0.0811359 0.98 0.979347 26.6648
47 0.0671919 0.0783265 0.982456 0.978947 27.2929
48 0.0658817 0.0772342 0.981754 0.977747 27.8119
49 0.0634615 0.0762576 0.983333 0.974947 28.3876
50 0.0622394 0.0710278 0.982321 0.981747 28.9067
Predicted Edible Actual Edible
Our prediction was correct. Success!
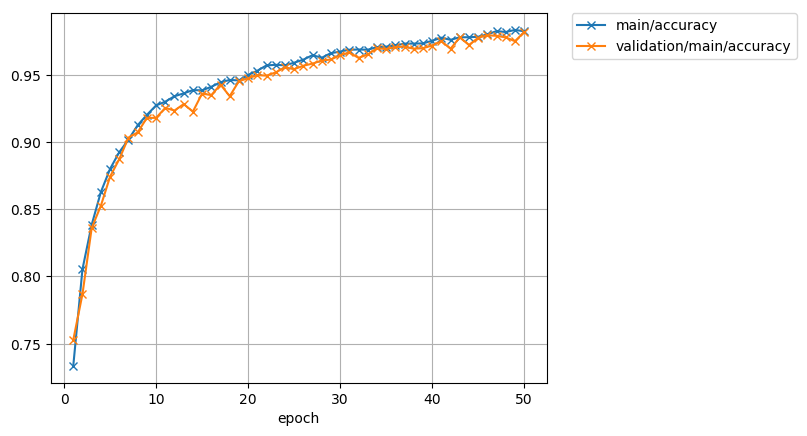
The loss function:
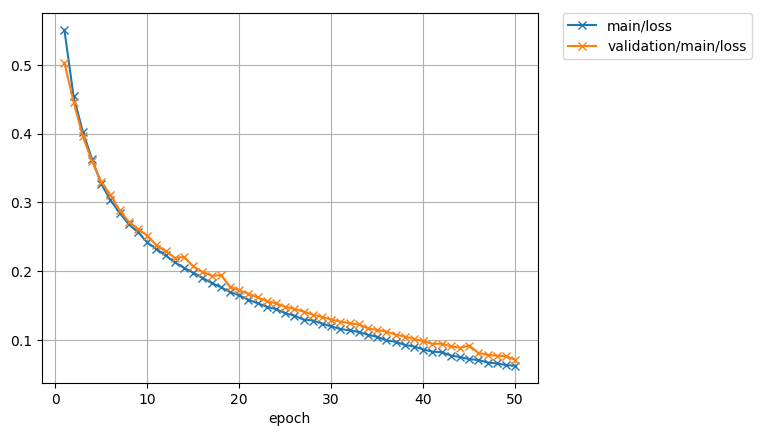
And the accuracy