Programming Models for Deep Learning¶
There are a lot of deep learning libraries, each comes with its own flavour. How can each flavour introduced by each library provide advantages or drawbacks in terms of system optimization and user experience? This article aims to compare these flavours in terms of programming models, discuss the fundamental advantages and drawbacks introduced by these models, and how we can learn from them.
We will focus on the programming model itself instead of the implementations. So this article is not about benchmarking deep learning libraries. Instead, we will divide the libraries into several categories in terms of what user interface they offer, and discuss how these styles of interface affect performance and flexibility of deep learning programs. The discussion in this article may not be specific to deep learning, but we will keep deep learning applications as our use-cases and goal of optimization.
Symbolic vs Imperative Programs¶
This is the first section to get started, the first thing we are going to compare is symbolic style programs vs imperative style programs. If you are a python or c++ programmer, it is likely you are already familiar with imperative programs. Imperative style programs conduct the computation as we run them. Most code you write in python is imperative, for example, the following numpy snippet.
import numpy as np
a = np.ones(10)
b = np.ones(10) * 2
c = b * a
d = c + 1
When the programs execute to c = b * a, it runs the actual computation. Symbolic programs are a bit different.
The following snippet is an equivalent symbolic style program you can write to achieve the same goal of calculating d.
A = Variable('A')
B = Variable('B')
C = B * A
D = C + Constant(1)
# compiles the function
f = compile(D)
d = f(A=np.ones(10), B=np.ones(10)*2)
The difference in symbolic programs is when C = B * A is executed, there is no actual computation happening.
Instead, these operations generate a computation graph (symbolic graph) that represents the computation it described.
The following picture gives a computation graph to compute D.
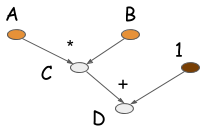
Most symbolic style programs contain, either explicitly or implicitly, a compile step.
This converts the computation graph into a function that can be called.
Then the real computation happens at the last step of the code. The major characteristic of symbolic programs
is the clear separation between the computation graph definition step, and the compile, running step.
Examples of imperative style deep learning libraries include Torch, Chainer and Minerva. While the examples of symbolic style deep learning libraries include Theano, CGT and Tensorflow. Libraries that use configuration files like cxxnet, caffe can also be viewed as symbolic style libraries, where the configuration file content defines the computation graph.
Now you know the two different programming models, let us start to compare them!
Imperative Programs are More Flexible¶
This is a general statement that may not apply strictly, but indeed imperative programs are usually more flexible than symbolic programs. If you are writing an imperative style programs in python, you are writing in python. However, if you are writing a symbolic program, it is different. Consider the following imperative program, think how you can translate this into a symbolic program.
a = 2
b = a + 1
d = np.zeros(10)
for i in range(d):
d += np.zeros(10)
You can find it is actually not easy, because there is a python for-loop that may not readily supported by the symbolic API. If you are writing a symbolic programs in python, you are NOT writing in python. Instead, you actually write a domain specific language defined by the symbolic API. The symbolic APIs are more powerful version of DSL that generates the computation graphs or configuration of neural nets. In that sense, the config-file input libraries are all symbolic.
Because imperative programs are actually more native than the symbolic ones, it is easier to use native language features
and inject them into computation flow. Such as printing out the values in the middle of computation, and use conditioning and loop in host language.
Symbolic Programs are More Efficient¶
As we can see from the discussion in previous section, imperative programs are usually more flexible and native to the host language. Why larger portion of deep learning libraries chose to be symbolic instead? The main reason is efficiency, both in terms of memory and runtime. Let us consider the same toy example used in the beginning of this section.
import numpy as np
a = np.ones(10)
b = np.ones(10) * 2
c = b * a
d = c + 1
...

Assume each cell in the array cost 8 bytes. How many memory do we need to cost if we are going to execute the above program in python console?
Let us do some math, we need memory for 4 arrays of size 10, that means we will need 4 * 10 * 8 = 320 bytes. On the other hand,
to execute the computation graph, we can re-use memory of C and D, to do the last computation in-place, this will give us 3 * 10 * 8 = 240
bytes instead.
Symbolic programs are more restricted. When the user call compile on D, the user tells the system that only the value of
D is needed. The intermediate values of computation, in our case C is invisible to the user.
This allows the symbolic programs to safely re-use the memory to do in-place computation.
Imperative programs, on the other hand, need to be prepared for all possible futures. If the above programs is executed in a python console, there is a possibility that any of these variables could be used in the future, this prevents the system to share the memory space of these variables.
Of course this argument is a bit idealized, since garbage collection can happen in imperative programs when things runs out of scope, and memory could be re-used. However, the constraint to be “prepared for all possible futures” indeed happens, and limits the optimizations we can do. This holds for non-trival cases such as gradient calculation, which we will be discussing in next section.
Another optimization that symbolic programs can do is operation folding. In the above programs, the multiplication and addition can be folded into one operation. Which is represented in the following graph. This means one GPU kernel will be executed(instead of two) if the computation runs on GPU. This is actually what we will do to hand crafted operations in optimized libraries such as cxxnet, caffe. Doing so will improve the computation efficiency.
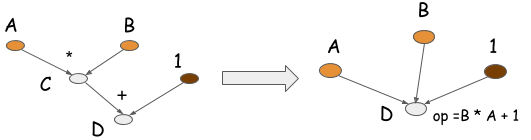
We cannot do that in imperative programs. Because the intermediate value can be reference some point in the future. The reason that such optimization is possible in symbolic programs, is that we get the entire computation graph, and a clear boundary on which value is needed and which is not. While imperative programs only operates on local operations and do not have such a clear boundary.
Case Study on Backprop and AutoDiff¶
In this section, we will compare the two programing models on the problem of auto differentiation, or backpropagation. Gradient calculation is actually the problem that all the deep learning library need to solve. It is possible to do gradient calculation in both imperative and symbolic style.
Let us start with the imperative programs. The following snippet is a minimum python code that does automatic differentiation on the toy example we discussed.
class array(object) :
"""Simple Array object that support autodiff."""
def __init__(self, value, name=None):
self.value = value
if name:
self.grad = lambda g : {name : g}
def __add__(self, other):
assert isinstance(other, int)
ret = array(self.value + other)
ret.grad = lambda g : self.grad(g)
return ret
def __mul__(self, other):
assert isinstance(other, array)
ret = array(self.value * other.value)
def grad(g):
x = self.grad(g * other.value)
x.update(other.grad(g * self.value))
return x
ret.grad = grad
return ret
# some examples
a = array(1, 'a')
b = array(2, 'b')
c = b * a
d = c + 1
print d.value
print d.grad(1)
# Results
# 3
# {'a': 2, 'b': 1}
In the above program, each array object contains a grad function(it is actually a closure).
When we run d.grad, it recursively invoke grad function of its inputs, backprops the gradient value back,
returns the gradient value of each inputs. This may looks a bit complicated. Let us consider the gradient calculation for
symbolic programs. The program below is an example of doing symbolic gradient calculation of the same task.
A = Variable('A')
B = Variable('B')
C = B * A
D = C + Constant(1)
# get gradient node.
gA, gB = D.grad(wrt=[A, B])
# compiles the gradient function.
f = compile([gA, gB])
grad_a, grad_b = f(A=np.ones(10), B=np.ones(10)*2)
The grad function of D generate a backward computation graph, and return a gradient node gA, gB.
They corresponds to the red nodes in the following figure.

What the imperative program did was actually the same as the symbolic way. It implicitly saves a backward
computation graph in the grad closure. When we invoked the d.grad, we start from d(D),
backtrace the graph to compute the gradient and collect the results back.
So we can find that in fact the gradient calculation in both symbolic and imperative programming follows the same
pattern. What is the difference between the two then? Again recall the “have to prepared for all possible futures”
requirement of imperative programs. If we are making an array library that support automatic differentiation,
we have to keep the grad closure along with the computation. This means all the history variables cannot be
garbage collected because they are referenced by variable d via function closure.
Now, what if when we only want to compute the value of d, but do not want the gradient value?
In symbolic programming, user declares the need by f=compiled([D]) instead. It also declares the boundary
of computation, telling the system I only want to compute the forward pass. As a result, the system can
free the memory of previous results, and share the memory between inputs and outputs.
Imagine now we are not running this toy example, but doing instead a deep neural net with n layers.
If we are only running forward pass, but not backward(gradient) pass, we will only need to allocate 2 copies of
temporal space to store values of intermediate layers, instead of n copies of them.
However because the imperative programs need to be prepared for the possible futures of getting gradient,
the intermediate values have to be stored, which requires n copies of temporal space.
As we can see the level of optimization comes with the restrictions of what user can do. The idea of symbolic programs is ask user to clearly specify the boundary of computation by compile or its equivalence. While the imperative programs prepares for all possible futures. The symbolic programs get a natural advantage by seeing more on what user wants and what user do not want.
Of course we can also enhance the imperative programs to impose restrictions. For example, one solution to above problem is to introduce a context variable. We can introduce a no gradient context variable, to switch the gradient calculation off. This brings a bit more restriction into the imperative programs, in trading for efficiency.
with context.NoGradient():
a = array(1, 'a')
b = array(2, 'b')
c = b * a
d = c + 1
However, the above example still have many possible futures, which means we cannot do the inplace calculation to re-use the memory in forward pass(a trick commonly used to reduce GPU memory usage). The techniques introduced in this section generates explicit backward pass. On some of the toolkits such as caffe, cxxnet. Backprop is done implicitly on the same graph. The discussions of this section also applies to these cases as well.
Most configuration file based libraries such as cxxnet, caffe are designed for one or two generic requirement. Get the activation of each layer, or get gradient of all the weights. Same problem stays for these libraries, the more generic operations the library have to support, the less optimization(memory sharing) we can do, based on the same data structure.
So as you can see the trade-off between restriction and flexibility stays for most cases.
Model Checkpoint¶
Being able to save a model and load it back later is important for most users. There are different ways to save your work.
Normally, to save a neural net, we need to save two things, a net configuration about structure of the neural net, and weights of neural net.
Being able to checkpoint the configuration is a plus for symbolic programs. Because the symbolic construction phase do not contain computation, we can directly serialize the computation graph, and load it back later, this solves the save configuration problem without introducing an additional layer.
A = Variable('A')
B = Variable('B')
C = B * A
D = C + Constant(1)
D.save('mygraph')
...
D2 = load('mygraph')
f = compile([D2])
# more operations
...
Because imperative programs executes as it describes the computation. We will have to save the code itself as the configuration, or build another
configuration layer on top of the imperative language.
Parameter Update¶
Most symbolic programs are data flow(computation) graphs. Dataflow graph can be used to descrie computation conveniently. However, it is not obvious how to use data flow graph to describe parameter updates, because parameter updates introduces mutation, which is not concept of data flow. What most symbolic programs do is to introduce a special update statement, to update some persistent states of the programs.
It is usually easier to write the parameter updates in imperative styles, especially when we need multiple updates that relates to each other. For symbolic programs, the update statement is also executed as we call them. So in that sense, most existing symbolic deep learning libraries also falls back to the imperative way to perform the updates, while using the symbolic way to do the gradient calculation.
There is no Strict Boundary¶
We have made the comparison between two programming styles. Some of the arguments made may not be strictly true, and there is no clear boundaries between the programming styles. For example, we can make a (JIT)compiler of python to compile imperative python programs, which gives us some of the advantage of global information hold in the symbolic programs. However, most of the principles holds true in general, and these constraints apply when we are making a deep learning libraries.
Big vs Small Operations¶
Now we have pass through the battlefield between symbolic and imperative programs. Let us start to talk about the operations supported by deep learning libraries. Usually there are two types of operations supported by different deep learning libraries.
- The big layer operations such as FullyConnected, BatchNormalize
- The small operations such as elementwise addition, multiplications. The libraries like cxxnet, caffe support layer level operations. While the libraries like Theano, Minerva support fine grained operations.
Smaller Operations can be More Flexible¶
This is quite natural, in a sense that we can always use smaller operations to compose bigger operations. For example, the sigmoid unit can be simply be composed by division and exponential.
sigmoid(x) = 1.0 / (1.0 + exp(-x))
If we have the smaller operations as building blocks, we can express most of the problems we want. For readers who are more familar with cxxnet, caffe style layers. These operations is not different from a layer, except that they are smaller.
SigmoidLayer(x) = EWiseDivisionLayer(1.0, AddScalarLayer(ExpLayer(-x), 1.0))
So the above expression becomes composition of three layers, with each defines their forward and backward(gradient) function. This offers us an advantage to build new layers quickly, because we only need to compose these things together.
Big Operations are More Efficient¶
As you can see directly composing up sigmoid layers means we need to have three layers of operation, instead of one.
SigmoidLayer(x) = EWiseDivisionLayer(1.0, AddScalarLayer(ExpLayer(-x), 1.0))
This will create overhead in terms of computation and memory (which could be optimized, with cost).
So the libraries like cxxnet, caffe take a different approach. To support more coarse grained operations such as BatchNormalization, and the SigmoidLayer directly. In each of these layers, the calculation kernel is handcrafted with one or only some CUDA kernel launches. This brings more efficiency to these implementations.
Compilation and Optimization¶
Can the small operations be optimized? Of course they can. This comes to the system optimization part of the compilation engine. There are two types of optimization that can be done on the computation graph
- The memory allocation optimization, to reuse memory of the intermediate computations.
- Operator fusion, to detect subgraph pattern such as the sigmoid and fuse them into a bigger operation kernel. The memory allocation optimization was actually not restricted to small operations graphs, but can also be applied to bigger operations graph as well.
However these optimization may not be essential for bigger operation libraries like cxxnet, caffe. As you never find the compilation step in them. Actually there is a (dumb) compilation step in these libraries, that basically translate the layers into a fixed forward, backprop execution plan, by running each operation one by one.
For computation graphs with smaller operations, these optimizations are crucial for performance. Because the operations are small, there are many subgraph patterns that can be matched. Also because the final generated operations may not be able to enumerated, an explicit recompilation of the kernels is required, as opposed to the fixed amount of pre-compiled kernels in the big operation libraries. This is the cause of compilation overhead of the symbolic libraries that support small operations. The requirement of compilation optimization also creates overhead of engineering for the libraries that solely support smaller operations.
Like in the symbolic vs imperative case. The bigger operation libraries “cheat” by asking user to provide restrictions(to the common layer provided), so user is actually the one that does the subgraph matching. This removes the compilation overhead to the real brain, which is usually not too bad.
Expression Template and Statically Typed Language¶
As we can see we always have a need to write small operations and compose them together. Libraries like caffe use hand-carfted kernels to build up these bigger blocks. Otheriwse user have to compose up smaller operations from python side.
Actually, there is a third choice, that works pretty well. This is called expression template. Basically, the idea is to use template programming to generate generic kernels from expression tree at compile time. You can refer to the Expression Template Tutorial for more details. CXXNet is a library that makes extensive use of expression template, this enables much shorter and more readable code, with matched performance with hand crafted kernels.
The difference between expression template and python kernel generation is that the expression evaluation is done at compile time of c++, with an existing type, so there is no additional runtime overhead. This is also in principle possible with other statically typed language that support template, however we have only seen this trick in C++ so far.
The expression template libraries creates a middle ground between python operations and hand crafted big kernels. To allow C++ users to craft efficient big operations by composing smaller operations together. Which is also a choice worth considering.
Mix The Flavours Together¶
Now we have compared the programming models, now comes the question of which you might want to choose. Before we doing so, we should emphasize the the comparison made in this article may not necessary have big impact depending on where the problems are.
Remember Amdahl’s law, if you are optimizing non performance critical part of your problem, you won’t get much of the performance gain.
As we can see usually there is a trade-off between efficiency, flexibility, engineering complexities. And usually different programming styles fits into different parts of the problems. For example, imperative programs are more natural for parameter update, and symbolic programs for gradient calculation.
What this article advocate is to mix the flavours together. Recall Amdahl’s law. Sometimes the part we want to be flexible are not necessarily performance crucial, and it is OK to be a bit sloppy to support more flexible interfaces. In machine learning, ensemble of different methods usually work better than a single one.
If the programming models can be mixed together in a correct way, we could also get better benefit than a single programming model. We will list some of the possible discussions here.
Symbolic and Imperative Programs¶
There are two ways to mix symbolic and imperative programs.
- Put imperative programs as part of symbolic programs as callbacks.
- Put symbolic programs as part of imperative programs.
What we usually observe is that it is usually helpful to write parameter updates in an imperative way, while the gradient calculations can be done more effectively in symbolic programs.
The mix of programs is actually happening in existing symbolic libraries, because python itself is imperative. For example, the following program mixes the symbolic part together with numpy(which is imperative).
A = Variable('A')
B = Variable('B')
C = B * A
D = C + Constant(1)
# compiles the function
f = compile(D)
d = f(A=np.ones(10), B=np.ones(10)*2)
d = d + 1.0
The idea is that the symbolic graphs are compiled into a function that can be executed imperatively. Whose internal is a blackbox to the user. This is exactly like writing c++ programs and exposing them to python, which we commonly do.
However, using numpy as imperative component might be undesirable, as the parameter memory resides on GPU. A better way might be supporting a GPU compatible imperative library that interacts with symbolic compiled functions, or provide limited amount of updating syntax via update statement in symbolic programs execution.
Small and Big Operations¶
Combining small and big operations is also possible, and actually we might have a good reason to do it. Consider applications such as changing a loss function or adding a few customized layers to an existing structure. What we usually can do is use big operations to compose up the existing components, and use smaller operations to build up the new parts.
Recall Amdahl’s law, usually these new components may not be the bottleneck of computation. As the performance critical part is already optimized by the bigger operations, it is even OK that we do not optimize these additional small operations at all, or only do a few memory optimization instead of operation fusion and directly running them.
Choose your Own Flavours¶
As we have compare the flavours of deep learning programs. The goal of this article is to list these choices and compare their trade-offs. There may not be a universal solution for all. But you can always choose your flavour, or combine the flavours you like to create more interesting and intelligent deep learning libraries.
Contribution to this Note¶
This note is part of our effort to open-source system design notes for deep learning libraries. You are more welcomed to contribute to this Note, by submitting a pull request.
