numpy.cov¶
- numpy.cov(m, y=None, rowvar=1, bias=0, ddof=None, fweights=None, aweights=None)[source]¶
Estimate a covariance matrix, given data and weights.
Covariance indicates the level to which two variables vary together. If we examine N-dimensional samples,
![X = [x_1, x_2, ... x_N]^T](../../_images/math/8d14fb48024fc0aaeed58a8b7e012bf142402c41.png) ,
then the covariance matrix element
,
then the covariance matrix element 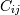 is the covariance of
is the covariance of
 and
and 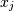 . The element
. The element  is the variance
of
is the variance
of  .
.See the notes for an outline of the algorithm.
Parameters: m : array_like
A 1-D or 2-D array containing multiple variables and observations. Each row of m represents a variable, and each column a single observation of all those variables. Also see rowvar below.
y : array_like, optional
An additional set of variables and observations. y has the same form as that of m.
rowvar : int, optional
If rowvar is non-zero (default), then each row represents a variable, with observations in the columns. Otherwise, the relationship is transposed: each column represents a variable, while the rows contain observations.
bias : int, optional
Default normalization is by (N - 1), where N corresponds to the number of observations given (unbiased estimate). If bias is 1, then normalization is by N. These values can be overridden by using the keyword ddof in numpy versions >= 1.5.
ddof : int, optional
If not None the default value implied by bias is overridden. Note that ddof=1 will return the unbiased estimate, even if both fweights and aweights are specified, and ddof=0 will return the simple average. See the notes for the details. The default value is None.
New in version 1.5.
fweights : array_like, int, optional
1-D array of integer freguency weights; the number of times each observation vector should be repeated.
New in version 1.10.
aweights : array_like, optional
1-D array of observation vector weights. These relative weights are typically large for observations considered “important” and smaller for observations considered less “important”. If ddof=0 the array of weights can be used to assign probabilities to observation vectors.
New in version 1.10.
Returns: out : ndarray
The covariance matrix of the variables.
See also
- corrcoef
- Normalized covariance matrix
Notes
Assume that the observations are in the columns of the observation array m and let f = fweights and a = aweights for brevity. The steps to compute the weighted covariance are as follows:
>>> w = f * a >>> v1 = np.sum(w) >>> v2 = np.sum(w * a) >>> m -= np.sum(m * w, axis=1, keepdims=True) / v1 >>> cov = np.dot(m * w, m.T) * v1 / (v1**2 - ddof * v2)
Note that when a == 1, the normalization factor v1 / (v1**2 - ddof * v2) goes over to 1 / (np.sum(f) - ddof) as it should.
Examples
Consider two variables,
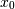 and
and 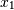 , which
correlate perfectly, but in opposite directions:
, which
correlate perfectly, but in opposite directions:>>> x = np.array([[0, 2], [1, 1], [2, 0]]).T >>> x array([[0, 1, 2], [2, 1, 0]])
Note how
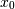 increases while
increases while 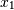 decreases. The covariance
matrix shows this clearly:
decreases. The covariance
matrix shows this clearly:>>> np.cov(x) array([[ 1., -1.], [-1., 1.]])
Note that element
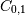 , which shows the correlation between
, which shows the correlation between
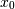 and
and 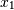 , is negative.
, is negative.Further, note how x and y are combined:
>>> x = [-2.1, -1, 4.3] >>> y = [3, 1.1, 0.12] >>> X = np.vstack((x,y)) >>> print np.cov(X) [[ 11.71 -4.286 ] [ -4.286 2.14413333]] >>> print np.cov(x, y) [[ 11.71 -4.286 ] [ -4.286 2.14413333]] >>> print np.cov(x) 11.71