numpy.random.rayleigh¶

numpy.random.rayleigh(scale=1.0, size=None)¶

Draw samples from a Rayleigh distribution.

The 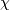$\chi$ and Weibull distributions are generalizations of the Rayleigh.

Parameters:

Parameters:	scale : scalar Scale, also equals the mode. Should be >= 0. size : int or tuple of ints, optional Output shape. If the given shape is, e.g., `(m, n, k)`, then `m * n * k` samples are drawn. Default is None, in which case a single value is returned.

scale : scalar

Scale, also equals the mode. Should be >= 0.

size : int or tuple of ints, optional

Output shape. If the given shape is, e.g., (m, n, k), then m * n * k samples are drawn. Default is None, in which case a single value is returned.

Notes

The probability density function for the Rayleigh distribution is

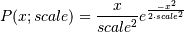
$P(x;scale) = \frac{x}{scale^2}e^{\frac{-x^2}{2 \cdotp scale^2}}$

The Rayleigh distribution would arise, for example, if the East and North components of the wind velocity had identical zero-mean Gaussian distributions. Then the wind speed would have a Rayleigh distribution.

References

[R259]

Brighton Webs Ltd., “Rayleigh Distribution,” http://www.brighton-webs.co.uk/distributions/rayleigh.asp

[R260]

Wikipedia, “Rayleigh distribution” http://en.wikipedia.org/wiki/Rayleigh_distribution

Examples

Draw values from the distribution and plot the histogram

>>> values = hist(np.random.rayleigh(3, 100000), bins=200, normed=True)

Wave heights tend to follow a Rayleigh distribution. If the mean wave height is 1 meter, what fraction of waves are likely to be larger than 3 meters?

>>> meanvalue = 1
>>> modevalue = np.sqrt(2 / np.pi) * meanvalue
>>> s = np.random.rayleigh(modevalue, 1000000)

The percentage of waves larger than 3 meters is:

>>> 100.*sum(s>3)/1000000.
0.087300000000000003