Lightweight, Lazy Trees

7.7

top ← prev up next →

Lightweight, Lazy Trees

Siddhartha Kasivajhula

Lightweight, general-purpose utilities for working with tree-structured data.

This module provides utilities to leverage the natural hierarchical structure of nested lists (and streams) to represent and perform computations on tree-structured data. The tree representation, in list form, is simply

(data child ...)

where each child has the same structure. A single-element stream represents a leaf node, containing only data and no children. Any sequence with this structure is treatable as a tree for the purposes of the utilities provided here. For example, the list

'(1 (2 (3) (4)) (5 (6)))

is a well-formed tree, with structure that could be visualized as:

procedure
(make-tree f node) → sequence?
f : (-> any/c sequence?)
node : any/c

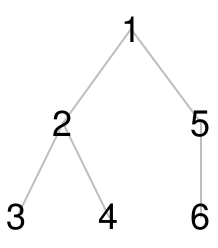
Construct a tree from a node (which could be any value) and a function f that yields the next level of the hierarchy (i.e. "children" or "parents") given an input node. The function f is recursively – and lazily – applied starting from node to yield a stream exhibiting the canonical tree structure.

Examples:

> (struct taxon (name children))
> (define dog (taxon "Dog" '()))
> (define cat (taxon "Cat" '()))
> (define mammal (taxon "Mammal" (list dog cat)))
> (->list (tree-traverse (make-tree taxon-children mammal)))
(list (taxon "Mammal" (list (taxon "Dog" '()) (taxon "Cat" '()))) (taxon "Dog" '()) (taxon "Cat" '()))

procedure
(tree-traverse t
[ #:order order
#:converse? converse?]) → sequence?
  t : sequence?
  order : (one-of/c 'pre 'post 'in 'level) = 'pre
  converse? : boolean? = #f

Traverse a tree using one of the standard traversal orders, i.e. preorder, postorder, in-order or level-order traversal. If converse? is true, then traverses right-to-left instead of left-to-right. Although these traversals are canonically defined for binary trees, trees with an arity greater than two are still supported, using trivial generalizations of the binary tree versions. For instance, an in-order traversal would visit a single child prior to visiting the parent, and then visit all of the remaining children of that parent. See here for some helpful animations of tree traversals.

Examples:

> (define t '(1 (2 (3) (4)) (5 (6))))
> (->list (tree-traverse #:order 'pre t))
'(1 2 3 4 5 6)
> (->list (tree-traverse #:converse? #t #:order 'pre t))
'(1 5 6 2 4 3)
> (->list (tree-traverse #:order 'post t))
'(3 4 2 6 5 1)
> (->list (tree-traverse #:order 'in t))
'(3 2 4 1 6 5)
> (->list (tree-traverse #:order 'level t))
'(1 2 5 3 4 6)
> (struct taxon (name children))
> (define dog (taxon "Dog" '()))
> (define cat (taxon "Cat" '()))
> (define mammal (taxon "Mammal" (list dog cat)))
> (define t (make-tree taxon-children mammal))
> (->list (map taxon-name (tree-traverse #:order 'pre t)))
'("Mammal" "Dog" "Cat")
> (->list (map taxon-name (tree-traverse #:order 'post t)))
'("Dog" "Cat" "Mammal")
> (->list (map taxon-name (tree-traverse #:order 'in t)))
'("Dog" "Mammal" "Cat")
> (->list (map taxon-name (tree-traverse #:order 'level t)))
'("Mammal" "Dog" "Cat")
> (->list (map taxon-name (tree-traverse #:converse? #t #:order 'pre t)))
'("Mammal" "Cat" "Dog")

procedure
(tree-map f t) → sequence?
f : (-> any/c any/c)
t : sequence?

Analogously to map, lazily maps each element in the tree under the function f.

Examples:

> (struct taxon (name children))
> (define dog (taxon "Dog" '()))
> (define cat (taxon "Cat" '()))
> (define mammal (taxon "Mammal" (list dog cat)))
> (define t (make-tree taxon-children mammal))
> (first (tree-map taxon-name t))
"Mammal"

procedure
(tree-filter f t) → sequence?
f : (-> any/c boolean?)
t : sequence?

Analogously to filter, lazily filters each element in the tree under the function f. If a node is filtered out, none of its descendants are present in the resulting tree.

Examples:

> (struct taxon (name children))
> (define dog (taxon "Dog" '()))
> (define cat (taxon "Cat" '()))
> (define mammal (taxon "Mammal" (list dog cat)))
> (define t (make-tree taxon-children mammal))
> (->list (tree-traverse (tree-map taxon-name (tree-filter (lambda (v) (/= (taxon-name v) "Dog")) t))))
'("Mammal" "Cat")

procedure
(tree-fold f
t
base
[ #:order order
#:converse? converse?
#:argument-order argument-order
#:with-steps? with-steps?]) → any/c
  f : (-> any/c any/c any/c)
  t : sequence?
  base : any/c
  order : (one-of/c 'pre 'post 'in 'level) = 'pre
  converse? : boolean? = #f
  argument-order : (one-of/c 'abb 'bab) = 'abb
  with-steps? : boolean? = #f

Analogously to fold, combines elements of the tree using the function f. While normal folds have a left or right direction, the direction of a tree fold is determined by the traversal order, which is specified via order.

Examples:

> (struct taxon (name children))
> (define dog (taxon "Dog" '()))
> (define cat (taxon "Cat" '()))
> (define mammal (taxon "Mammal" (list dog cat)))
> (define t (make-tree taxon-children mammal))
> (tree-fold (lambda (x xs) (.. (taxon-name x) xs)) t "")
"CatDogMammal"
> (tree-fold #:order 'post (lambda (x xs) (.. (taxon-name x) xs)) t "")
"MammalCatDog"

top ← prev up next →