scipy.interpolate.LSQUnivariateSpline

class scipy.interpolate.LSQUnivariateSpline(x, y, t, w=None, bbox=[None, None], k=3, ext=0, check_finite=False)

One-dimensional spline with explicit internal knots.

Fits a spline y = spl(x) of degree k to the provided x, y data. t specifies the internal knots of the spline

Parameters:

x : (N,) array_like

Input dimension of data points – must be increasing

y : (N,) array_like

Input dimension of data points

t : (M,) array_like

interior knots of the spline. Must be in ascending order and:

bbox[0] < t[0] < ... < t[-1] < bbox[-1]

w : (N,) array_like, optional

weights for spline fitting. Must be positive. If None (default), weights are all equal.

bbox : (2,) array_like, optional

2-sequence specifying the boundary of the approximation interval. If None (default), bbox = [x[0], x[-1]].

k : int, optional

Degree of the smoothing spline. Must be 1 <= k <= 5. Default is k=3, a cubic spline.

ext : int or str, optional

Controls the extrapolation mode for elements not in the interval defined by the knot sequence.

• if ext=0 or ‘extrapolate’, return the extrapolated value.
• if ext=1 or ‘zeros’, return 0
• if ext=2 or ‘raise’, raise a ValueError
• if ext=3 of ‘const’, return the boundary value.

The default value is 0.

check_finite : bool, optional

Whether to check that the input arrays contain only finite numbers. Disabling may give a performance gain, but may result in problems (crashes, non-termination or non-sensical results) if the inputs do contain infinities or NaNs. Default is False.

Raises:

ValueError

If the interior knots do not satisfy the Schoenberg-Whitney conditions

See also

UnivariateSpline

Superclass – knots are specified by setting a smoothing condition

InterpolatedUnivariateSpline

spline passing through all points

splrep

An older, non object-oriented wrapping of FITPACK

splev, sproot, splint, spalde

BivariateSpline

A similar class for two-dimensional spline interpolation

Notes

The number of data points must be larger than the spline degree k.

Knots t must satisfy the Schoenberg-Whitney conditions, i.e., there must be a subset of data points x[j] such that t[j] < x[j] < t[j+k+1], for j=0, 1,...,n-k-2.

Examples

>>> from scipy.interpolate import LSQUnivariateSpline
>>> import matplotlib.pyplot as plt
>>> x = np.linspace(-3, 3, 50)
>>> y = np.exp(-x**2) + 0.1 * np.random.randn(50)

Fit a smoothing spline with a pre-defined internal knots:

>>> t = [-1, 0, 1]
>>> spl = LSQUnivariateSpline(x, y, t)

>>> xs = np.linspace(-3, 3, 1000)
>>> plt.plot(x, y, 'ro', ms=5)
>>> plt.plot(xs, spl(xs), 'g-', lw=3)
>>> plt.show()

(Source code)

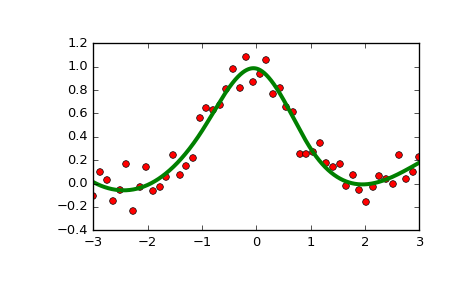
Check the knot vector:

>>> spl.get_knots()
array([-3., -1., 0., 1., 3.])

Methods

__call__(x[, nu, ext])	Evaluate spline (or its nu-th derivative) at positions x.
antiderivative([n])	Construct a new spline representing the antiderivative of this spline.
derivative([n])	Construct a new spline representing the derivative of this spline.
derivatives(x)	Return all derivatives of the spline at the point x.
get_coeffs()	Return spline coefficients.
get_knots()	Return positions of interior knots of the spline.
get_residual()	Return weighted sum of squared residuals of the spline approximation.
integral(a, b)	Return definite integral of the spline between two given points.
roots()	Return the zeros of the spline.
set_smoothing_factor(s)	Continue spline computation with the given smoothing factor s and with the knots found at the last call.