Solving Beam Bending Problems using Singularity Functions¶
To make this document easier to read, enable pretty printing:
>>> from sympy import *
>>> x, y, z = symbols('x y z')
>>> init_printing(use_unicode=True, wrap_line=False)
Beam¶
A planar beam is a structural element that is capable of withstanding load through resistance to internal shear and bending. Beams are characterized by their length, constraints, cross-sectional second moment of area, and elastic modulus. In SymPy, 2D beam objects are constructed by specifying the following properties:
Length
Elastic Modulus
Second Moment of Area
Variable : A symbol representing the location along the beam’s length. By default, this is set to
Symbol(x).- Boundary Conditions
bc_slope : Boundary conditions for slope.
bc_deflection : Boundary conditions for deflection.
Load Distribution
Once the above are specified, the following methods are used to compute useful information about the loaded beam:
solve_for_reaction_loads()shear_force()bending_moment()slope()
Examples¶
Below are examples of a variety two dimensional beam bending problems.
Example 1¶
A cantilever beam 9 meters in length has a distributed constant load of 8 kN/m applied downward from the fixed end over a 5 meter distance. A counterclockwise moment of 50 kN-m is applied 5 meters from the fixed end. Lastly, a downward point load of 12 kN is applied at the free end of the beam.
y
^
|
\\\\|
\\\\| 8 kN/m
\\\\|_________________
\\\\|| | | | | | | | | 12 kN
\\\\|V V V V V V V V V |
\\\\|________________|_______________V
\\\\| | |
\\\\o - - - - - - - -⭯ 50 kN-m - - - | - - -> x
\\\\|________________|_______________|
\\\\| :
\\\\|----------------|---------------|
5.0 m 4.0 m
Note
The user is free to choose their own sign convention. In this case the upward forces and counterclockwise bending moment being positive.
The beam must be initialized with the length, modulus of elasticity, and the second moment of area. These quantities can be symbols or numbers.
>>> from sympy.physics.continuum_mechanics.beam import Beam
>>> E, I = symbols('E, I')
>>> b = Beam(9, E, I)
The three loads are applied to the beam using the apply_load() method. This
method supports point forces, point moments, and polynomial distributed loads
of any order, i.e. \(c, cx, cx^2, cx^3, \ldots\).
The 12 kN point load is in the negative direction, at the location of 9 meters, and the polynomial order is specified as -1:
>>> b.apply_load(-12, 9, -1)
The load attribute can then be used to access the loading function in
singularity function form:
>>> b.load
-1
-12⋅<x - 9>
Similarly, the positive moment can be applied with a polynomial order -2:
>>> b.apply_load(50, 5, -2)
The distributed load is of order 0 and spans x=0 to x=5:
>>> b.apply_load(-8, 0, 0, end=5)
The fixed end imposes two boundary conditions: 1) no vertical deflection and 2) no rotation. These are specified by appending tuples of x values and the corresponding deflection or slope values:
>>> b.bc_deflection.append((0, 0))
>>> b.bc_slope.append((0, 0))
These boundary conditions introduce an unknown reaction force and moment which need to be applied to the beam to maintain static equilibrium:
>>> R, M = symbols('R, M')
>>> b.apply_load(R, 0, -1)
>>> b.apply_load(M, 0, -2)
>>> b.load
-2 -1 0 -2 0 -1
M⋅<x> + R⋅<x> - 8⋅<x> + 50⋅<x - 5> + 8⋅<x - 5> - 12⋅<x - 9>
These two variables can be solved for in terms of the applied loads and the final loading can be displayed:
>>> b.solve_for_reaction_loads(R, M)
>>> b.reaction_loads
{M: -258, R: 52}
>>> b.load
-2 -1 0 -2 0 -1
- 258⋅<x> + 52⋅<x> - 8⋅<x> + 50⋅<x - 5> + 8⋅<x - 5> - 12⋅<x - 9>
At this point, the beam is fully defined and the internal shear and bending moments are calculated like so:
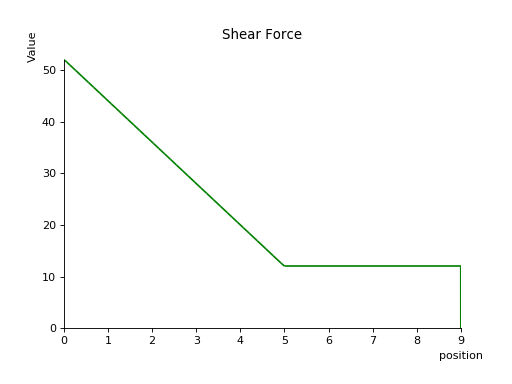
>>> b.shear_force()
-1 0 1 -1 1 0
- 258⋅<x> + 52⋅<x> - 8⋅<x> + 50⋅<x - 5> + 8⋅<x - 5> - 12⋅<x - 9>
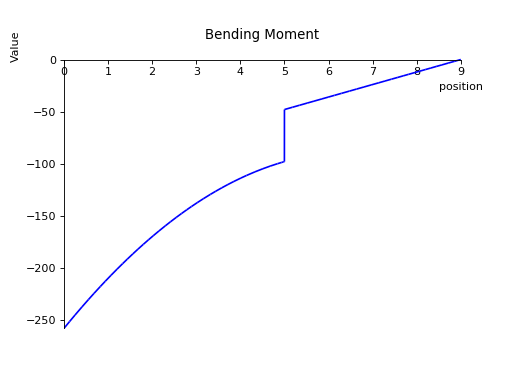
>>> b.bending_moment()
0 1 2 0 2 1
- 258⋅<x> + 52⋅<x> - 4⋅<x> + 50⋅<x - 5> + 4⋅<x - 5> - 12⋅<x - 9>
These can be visualized by calling the respective plot methods:
>>> b.plot_shear_force() # doctest: +SKIP
>>> b.plot_bending_moment() # doctest: +SKIP
The beam will deform under load and the slope and deflection can be determined with:
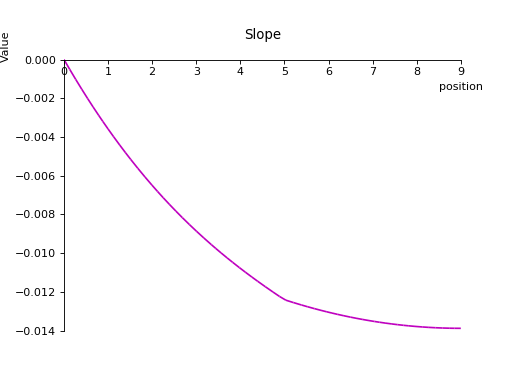
>>> b.slope()
3 3
1 2 4⋅<x> 1 4⋅<x - 5> 2
- 258⋅<x> + 26⋅<x> - ────── + 50⋅<x - 5> + ────────── - 6⋅<x - 9>
3 3
─────────────────────────────────────────────────────────────────────
E⋅I
>>> b.deflection()
3 4 4
2 26⋅<x> <x> 2 <x - 5> 3
- 129⋅<x> + ─────── - ──── + 25⋅<x - 5> + ──────── - 2⋅<x - 9>
3 3 3
─────────────────────────────────────────────────────────────────
E⋅I
The slope and deflection of the beam can be plotted so long as numbers are provided for the modulus and second moment:
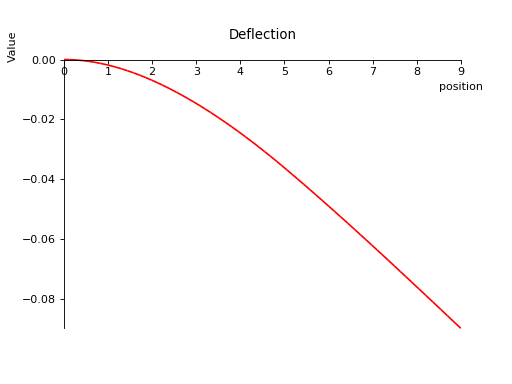
>>> b.plot_slope(subs={E: 20E9, I: 3.25E-6}) # doctest: +SKIP
>>> b.plot_deflection(subs={E: 20E9, I: 3.25E-6}) # doctest: +SKIP
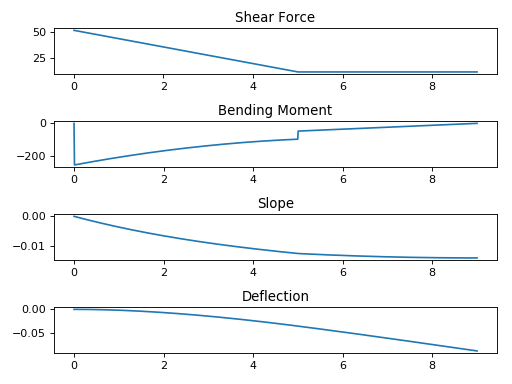
All of the plots can be shown in one figure with:
>>> b.plot_loading_results(subs={E: 20E9, I: 3.25E-6}) # doctest: +SKIP
Example 2¶
There is a beam of length 30 meters. A moment of magnitude 120 Nm is applied in the clockwise direction at the end of the beam. A pointload of magnitude 8 N is applied from the top of the beam at the starting point. There are two simple supports below the beam. One at the end and another one at a distance of 10 meters from the start. The deflection is restricted at both the supports.
|| 8 N ⭯ 120 Nm
\/______________________________________________|
|_______________________________________________|
/\ /\
|------------|---------------------------------|
10 m 20 m
Note
Using the sign convention of upward forces and counterclockwise moment being positive.
>>> from sympy.physics.continuum_mechanics.beam import Beam
>>> from sympy import symbols
>>> E, I = symbols('E, I')
>>> R1, R2 = symbols('R1, R2')
>>> b = Beam(30, E, I)
>>> b.apply_load(-8, 0, -1)
>>> b.apply_load(R1, 10, -1)
>>> b.apply_load(R2, 30, -1)
>>> b.apply_load(120, 30, -2)
>>> b.bc_deflection.append((10, 0))
>>> b.bc_deflection.append((30, 0))
>>> b.solve_for_reaction_loads(R1, R2)
>>> b.reaction_loads
{R₁: 6, R₂: 2}
>>> b.load
-1 -1 -2 -1
- 8⋅<x> + 6⋅<x - 10> + 120⋅<x - 30> + 2⋅<x - 30>
>>> b.shear_force()
0 0 -1 0
- 8⋅<x> + 6⋅<x - 10> + 120⋅<x - 30> + 2⋅<x - 30>
>>> b.bending_moment()
1 1 0 1
- 8⋅<x> + 6⋅<x - 10> + 120⋅<x - 30> + 2⋅<x - 30>
>>> b.slope()
2 2 1 2 4000
- 4⋅<x> + 3⋅<x - 10> + 120⋅<x - 30> + <x - 30> + ────
3
─────────────────────────────────────────────────────────
E⋅I
>>> b.deflection()
3 3
4000⋅x 4⋅<x> 3 2 <x - 30>
────── - ────── + <x - 10> + 60⋅<x - 30> + ───────── - 12000
3 3 3
──────────────────────────────────────────────────────────────
E⋅I
Example 3¶
A beam of length 6 meters is having a roller support at the start and a hinged support at the end. A counterclockwise moment of 1.5 kN-m is applied at the mid of the beam. A constant distributed load of 3 kN/m and a ramp load of 1 kN/m is applied from the mid till the end of the beam.
ramp load = 1 KN/m
constant load = 3 KN/m
|------------------------|
⭯ 1.5 KN-m
______________________|________________________
|_______________________________________________|
o | /\
|----------------------|-----------------------|
3.0 m 3.0 m
Note
Using the sign convention of upward forces and counterclockwise moment being positive.
>>> from sympy.physics.continuum_mechanics.beam import Beam
>>> from sympy import symbols
>>> E, I = symbols('E, I')
>>> R1, R2 = symbols('R1, R2')
>>> b = Beam(6, E, I)
>>> b.apply_load(R1, 0, -1)
>>> b.apply_load(1.5, 3, -2)
>>> b.apply_load(-3, 3, 0)
>>> b.apply_load(-1, 3, 1)
>>> b.apply_load(R2, 6, -1)
>>> b.bc_deflection.append((0, 0))
>>> b.bc_deflection.append((6, 0))
>>> b.solve_for_reaction_loads(R1, R2)
>>> b.reaction_loads
{R₁: 2.75, R₂: 10.75}
>>> b.load
-1 -2 0 1 -1
2.75⋅<x> + 1.5⋅<x - 3> - 3⋅<x - 3> - <x - 3> + 10.75⋅<x - 6>
>>> b.shear_force()
2
0 -1 1 <x - 3> 0
2.75⋅<x> + 1.5⋅<x - 3> - 3⋅<x - 3> - ──────── + 10.75⋅<x - 6>
2
>>> b.bending_moment()
2 3
1 0 3⋅<x - 3> <x - 3> 1
2.75⋅<x> + 1.5⋅<x - 3> - ────────── - ──────── + 10.75⋅<x - 6>
2 6
>>> b.slope()
3 4
2 1 <x - 3> <x - 3> 2
1.375⋅<x> + 1.5⋅<x - 3> - ──────── - ──────── + 5.375⋅<x - 6> - 15.6
2 24
───────────────────────────────────────────────────────────────────────
E⋅I
>>> b.deflection()
4 5
3 2 <x - 3> <x - 3> 3
-15.6⋅x + 0.458333333333333⋅<x> + 0.75⋅<x - 3> - ──────── - ──────── + 1.79166666666667⋅<x - 6>
8 120
──────────────────────────────────────────────────────────────────────────────────────────────────
E⋅I
Example 4¶
An overhanging beam of length 8 meters is pinned at 1 meter from starting point and supported by a roller 1 meter before the other end. It is subjected to a distributed constant load of 10 KN/m from the starting point till 2 meters away from it. Two pointloads of 20KN and 8KN are applied at 5 meters and 7.5 meters away from the starting point respectively.
---> x
|
v y
10 KN/m
_____________ 20 KN 8 KN
| | | | | | | | |
V V V V V V V V V
_______________________________________________
|_______________________________________________|
/\ O
|-----|------|-----------------|----------|--|--|
1m 1m 3m 2m .5m .5m
>>> from sympy.physics.continuum_mechanics.beam import Beam
>>> from sympy import symbols
>>> E,I,M,V = symbols('E I M V')
>>> b = Beam(8, E, I)
>>> E,I,R1,R2 = symbols('E I R1 R2')
>>> b.apply_load(R1, 1, -1)
>>> b.apply_load(R2, 7, -1)
>>> b.apply_load(10, 0, 0, end=2)
>>> b.apply_load(20, 5, -1)
>>> b.apply_load(8, 7.5, -1)
>>> b.solve_for_reaction_loads(R1, R2)
>>> b.reaction_loads
{R₁: -26.0, R₂: -22.0}
>>> b.load
0 -1 0 -1 -1 -1
10⋅<x> - 26.0⋅<x - 1> - 10⋅<x - 2> + 20⋅<x - 5> - 22.0⋅<x - 7> + 8⋅<x - 7.5>
>>> b.shear_force()
1 0 1 0 0 0
10⋅<x> - 26.0⋅<x - 1> - 10⋅<x - 2> + 20⋅<x - 5> - 22.0⋅<x - 7> + 8⋅<x - 7.5>
>>> b.bending_moment()
2 1 2 1 1 1
5⋅<x> - 26.0⋅<x - 1> - 5⋅<x - 2> + 20⋅<x - 5> - 22.0⋅<x - 7> + 8⋅<x - 7.5>
>>> b.bc_deflection = [(1, 0), (7, 0)]
>>> b.slope()
3 3
5⋅<x> 2 5⋅<x - 2> 2 2 2
────── - 13.0⋅<x - 1> - ────────── + 10⋅<x - 5> - 11.0⋅<x - 7> + 4⋅<x - 7.5> + 28.2916666666667
3 3
───────────────────────────────────────────────────────────────────────────────────────────────────
E⋅I
>>> b.deflection()
4 4 3 3
5⋅<x> 3 5⋅<x - 2> 10⋅<x - 5> 3 4⋅<x - 7.5>
28.2916666666667⋅x + ────── - 4.33333333333333⋅<x - 1> - ────────── + ─────────── - 3.66666666666667⋅<x - 7> + ──────────── - 28.7083333333333
12 12 3 3
────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
E⋅I
Example 5¶
A cantilever beam of length 6 meters is under downward distributed constant load with magnitude of 4.0 KN/m from starting point till 2 meters away from it. A ramp load of 1 kN/m applied from the mid till the end of the beam. A point load of 12KN is also applied in same direction 4 meters away from start.
---> x .
| . |
v y 12 KN . | |
| . | | |
V . | | | |
\\\\| 4 KN/m . | | | | |
\\\\|___________ . 1 KN/m | |
\\\\|| | | | | | . V V V V V V V
\\\\|V V V V V V |---------------|
\\\\|________________________________
\\\\|________________________________|
\\\\| : : :
\\\\|----------|-----|----|----------|
2.0 m 1m 1m 2.0 m
>>> from sympy.physics.continuum_mechanics.beam import Beam
>>> from sympy import symbols
>>> E,I,M,V = symbols('E I M V')
>>> b = Beam(6, E, I)
>>> b.apply_load(V, 0, -1)
>>> b.apply_load(M, 0, -2)
>>> b.apply_load(4, 0, 0, end=2)
>>> b.apply_load(12, 4, -1)
>>> b.apply_load(1, 3, 1, end=6)
>>> b.solve_for_reaction_loads(V, M)
>>> b.reaction_loads
{M: 157/2, V: -49/2}
>>> b.load
-2 -1
157⋅<x> 49⋅<x> 0 0 1 -1 0 1
───────── - ──────── + 4⋅<x> - 4⋅<x - 2> + <x - 3> + 12⋅<x - 4> - 3⋅<x - 6> - <x - 6>
2 2
>>> b.shear_force()
-1 0 2 2
157⋅<x> 49⋅<x> 1 1 <x - 3> 0 1 <x - 6>
───────── - ─────── + 4⋅<x> - 4⋅<x - 2> + ──────── + 12⋅<x - 4> - 3⋅<x - 6> - ────────
2 2 2 2
>>> b.bending_moment()
0 1 3 2 3
157⋅<x> 49⋅<x> 2 2 <x - 3> 1 3⋅<x - 6> <x - 6>
──────── - ─────── + 2⋅<x> - 2⋅<x - 2> + ──────── + 12⋅<x - 4> - ────────── - ────────
2 2 6 2 6
>>> b.bc_deflection = [(0, 0)]
>>> b.bc_slope = [(0, 0)]
>>> b.slope()
1 2 3 3 4 3 4
157⋅<x> 49⋅<x> 2⋅<x> 2⋅<x - 2> <x - 3> 2 <x - 6> <x - 6>
──────── - ─────── + ────── - ────────── + ──────── + 6⋅<x - 4> - ──────── - ────────
2 4 3 3 24 2 24
──────────────────────────────────────────────────────────────────────────────────────
E⋅I
>>> b.deflection()
2 3 4 4 5 4 5
157⋅<x> 49⋅<x> <x> <x - 2> <x - 3> 3 <x - 6> <x - 6>
──────── - ─────── + ──── - ──────── + ──────── + 2⋅<x - 4> - ──────── - ────────
4 12 6 6 120 8 120
──────────────────────────────────────────────────────────────────────────────────
E⋅I
Example 6¶
An overhanging beam of length 11 meters is subjected to a distributed constant load of 2 KN/m from 2 meters away from the starting point till 6 meters away from it. It is pinned at the starting point and is resting over a roller 8 meters away from that end. Also a counterclockwise moment of 5 KN-m is applied at the overhanging end.
2 KN/m ---> x
_________________ |
| | | | | | | | | v y
V V V V V V V V V ⭯ 5 KN-m
____________________________________________________|
O____________________________________________________|
/ \ /\
|--------|----------------|----------|---------------|
2m 4m 2m 3m
>>> R1, R2 = symbols('R1, R2')
>>> E, I = symbols('E, I')
>>> b = Beam(11, E, I)
>>> b.apply_load(R1, 0, -1)
>>> b.apply_load(2, 2, 0, end=6)
>>> b.apply_load(R2, 8, -1)
>>> b.apply_load(5, 11, -2)
>>> b.solve_for_reaction_loads(R1, R2)
>>> b.reaction_loads
{R₁: -37/8, R₂: -27/8}
>>> b.load
-1 -1
37⋅<x> 0 0 27⋅<x - 8> -2
- ──────── + 2⋅<x - 2> - 2⋅<x - 6> - ──────────── + 5⋅<x - 11>
8 8
>>> b.shear_force()
0 0
37⋅<x> 1 1 27⋅<x - 8> -1
- ─────── + 2⋅<x - 2> - 2⋅<x - 6> - ─────────── + 5⋅<x - 11>
8 8
>>> b.bending_moment()
1 1
37⋅<x> 2 2 27⋅<x - 8> 0
- ─────── + <x - 2> - <x - 6> - ─────────── + 5⋅<x - 11>
8 8
>>> b.bc_deflection = [(0, 0), (8, 0)]
>>> b.slope()
2 3 3 2
37⋅<x> <x - 2> <x - 6> 27⋅<x - 8> 1
- ─────── + ──────── - ──────── - ─────────── + 5⋅<x - 11> + 36
16 3 3 16
────────────────────────────────────────────────────────────────
E⋅I
>>> b.deflection()
3 4 4 3 2
37⋅<x> <x - 2> <x - 6> 9⋅<x - 8> 5⋅<x - 11>
36⋅x - ─────── + ──────── - ──────── - ────────── + ───────────
48 12 12 16 2
───────────────────────────────────────────────────────────────
E⋅I
Example 7¶
There is a beam of length l, fixed at both ends. A concentrated point load
of magnitude F is applied in downward direction at mid-point of the
beam.
^ y
|
---> x
\\\\| F |\\\\
\\\\| | |\\\\
\\\\| V |\\\\
\\\\|_____________________________________|\\\\
\\\\|_____________________________________|\\\\
\\\\| : |\\\\
\\\\| : |\\\\
\\\\|------------------|------------------|\\\\
l/2 l/2
>>> from sympy.physics.continuum_mechanics.beam import Beam
>>> from sympy import symbols
>>> E, I, F = symbols('E I F')
>>> l = symbols('l', positive=True)
>>> b = Beam(l, E, I)
>>> R1,R2 = symbols('R1 R2')
>>> M1, M2 = symbols('M1, M2')
>>> b.apply_load(R1, 0, -1)
>>> b.apply_load(M1, 0, -2)
>>> b.apply_load(R2, l, -1)
>>> b.apply_load(M2, l, -2)
>>> b.apply_load(-F, l/2, -1)
>>> b.bc_deflection = [(0, 0),(l, 0)]
>>> b.bc_slope = [(0, 0),(l, 0)]
>>> b.solve_for_reaction_loads(R1, R2, M1, M2)
>>> b.reaction_loads
⎧ -F⋅l F⋅l F F⎫
⎨M₁: ─────, M₂: ───, R₁: ─, R₂: ─⎬
⎩ 8 8 2 2⎭
>>> b.load
-2 -2 -1 -1 -1
F⋅l⋅<x> F⋅l⋅<-l + x> F⋅<x> l F⋅<-l + x>
- ───────── + ────────────── + ─────── - F⋅<- ─ + x> + ────────────
8 8 2 2 2
>>> b.shear_force()
-1 -1 0 0 0
F⋅l⋅<x> F⋅l⋅<-l + x> F⋅<x> l F⋅<-l + x>
- ───────── + ────────────── + ────── - F⋅<- ─ + x> + ───────────
8 8 2 2 2
>>> b.bending_moment()
0 0 1 1 1
F⋅l⋅<x> F⋅l⋅<-l + x> F⋅<x> l F⋅<-l + x>
- ──────── + ───────────── + ────── - F⋅<- ─ + x> + ───────────
8 8 2 2 2
>>> b.slope()
2
l
1 1 2 F⋅<- ─ + x> 2
F⋅l⋅<x> F⋅l⋅<-l + x> F⋅<x> 2 F⋅<-l + x>
- ──────── + ───────────── + ────── - ──────────── + ───────────
8 8 4 2 4
────────────────────────────────────────────────────────────────
E⋅I
>>> b.deflection()
3
l
2 2 3 F⋅<- ─ + x> 3
F⋅l⋅<x> F⋅l⋅<-l + x> F⋅<x> 2 F⋅<-l + x>
- ──────── + ───────────── + ────── - ──────────── + ───────────
16 16 12 6 12
────────────────────────────────────────────────────────────────
E⋅I
Example 8¶
There is a beam of length 4*l, having a hinge connector at the middle. It
is having a fixed support at the start and also has two rollers at a distance
of l and 4*l from the starting point. A concentrated point load P is also
applied at a distance of 3*l from the starting point.
---> x
\\\\| P |
\\\\| | v y
\\\\| V
\\\\|_____________________ _______________________
\\\\|_____________________O_______________________|
\\\\| /\ : /\
\\\\| oooo : oooo
\\\\|----------|-----------|----------|-----------|
l l l l
>>> from sympy.physics.continuum_mechanics.beam import Beam
>>> from sympy import symbols
>>> E, I = symbols('E I')
>>> l = symbols('l', positive=True)
>>> R1, M1, R2, R3, P = symbols('R1 M1 R2 R3 P')
>>> b1 = Beam(2*l, E, I)
>>> b2 = Beam(2*l, E, I)
>>> b = b1.join(b2, "hinge")
>>> b.apply_load(M1, 0, -2)
>>> b.apply_load(R1, 0, -1)
>>> b.apply_load(R2, l, -1)
>>> b.apply_load(R3, 4*l, -1)
>>> b.apply_load(P, 3*l, -1)
>>> b.bc_slope = [(0, 0)]
>>> b.bc_deflection = [(0, 0), (l, 0), (4*l, 0)]
>>> b.solve_for_reaction_loads(M1, R1, R2, R3)
>>> b.reaction_loads
⎧ -P⋅l 3⋅P -5⋅P -P ⎫
⎨M₁: ─────, R₁: ───, R₂: ─────, R₃: ───⎬
⎩ 4 4 4 2 ⎭
>>> b.load
-2 -1 -1 -1
P⋅l⋅<x> 3⋅P⋅<x> 5⋅P⋅<-l + x> -1 P⋅<-4⋅l + x>
- ───────── + ───────── - ────────────── + P⋅<-3⋅l + x> - ──────────────
4 4 4 2
>>> b.shear_force()
-1 0 0 0
P⋅l⋅<x> 3⋅P⋅<x> 5⋅P⋅<-l + x> 0 P⋅<-4⋅l + x>
- ───────── + ──────── - ───────────── + P⋅<-3⋅l + x> - ─────────────
4 4 4 2
>>> b.bending_moment()
0 1 1 1
P⋅l⋅<x> 3⋅P⋅<x> 5⋅P⋅<-l + x> 1 P⋅<-4⋅l + x>
- ──────── + ──────── - ───────────── + P⋅<-3⋅l + x> - ─────────────
4 4 4 2
>>> b.slope()
⎛ 2 2 2 2⎞ ⎛ 1 2 2 2⎞ ⎛ 1 2 2 2⎞
⎜5⋅P⋅l P⋅<-2⋅l + x> P⋅<-3⋅l + x> P⋅<-4⋅l + x> ⎟ 0 ⎜ P⋅l⋅<x> 3⋅P⋅<x> 5⋅P⋅<-l + x> P⋅<-2⋅l + x> ⎟ 0 ⎜ P⋅l⋅<x> 3⋅P⋅<x> 5⋅P⋅<-l + x> P⋅<-2⋅l + x> ⎟ 0
⎜────── - ───────────── + ───────────── - ─────────────⎟⋅<-2⋅l + x> ⎜- ──────── + ──────── - ───────────── + ─────────────⎟⋅<x> ⎜- ──────── + ──────── - ───────────── + ─────────────⎟⋅<-2⋅l + x>
⎝ 48 4 2 4 ⎠ ⎝ 4 8 8 4 ⎠ ⎝ 4 8 8 4 ⎠
──────────────────────────────────────────────────────────────────── + ──────────────────────────────────────────────────────────── - ───────────────────────────────────────────────────────────────────
E⋅I E⋅I E⋅I
>>> b.deflection()
⎛ 2 3 3 3⎞ ⎛ 2 3 3 3⎞ ⎛ 3 2 3 3 3⎞
⎜ P⋅l⋅<x> P⋅<x> 5⋅P⋅<-l + x> P⋅<-2⋅l + x> ⎟ 0 ⎜ P⋅l⋅<x> P⋅<x> 5⋅P⋅<-l + x> P⋅<-2⋅l + x> ⎟ 0 ⎜7⋅P⋅l 5⋅P⋅l ⋅(-2⋅l + x) P⋅<-2⋅l + x> P⋅<-3⋅l + x> P⋅<-4⋅l + x> ⎟ 0
⎜- ──────── + ────── - ───────────── + ─────────────⎟⋅<x> ⎜- ──────── + ────── - ───────────── + ─────────────⎟⋅<-2⋅l + x> ⎜────── + ───────────────── - ───────────── + ───────────── - ─────────────⎟⋅<-2⋅l + x>
⎝ 8 8 24 12 ⎠ ⎝ 8 8 24 12 ⎠ ⎝ 24 48 12 6 12 ⎠
────────────────────────────────────────────────────────── - ───────────────────────────────────────────────────────────────── + ────────────────────────────────────────────────────────────────────────────────────────
E⋅I E⋅I E⋅I
Example 9¶
There is a cantilever beam of length 4 meters. For first 2 meters
its moment of inertia is 1.5*I and I for the other end.
A pointload of magnitude 20 N is applied from the top at its free end.
---> x
\\\\| |
\\\\| 20 N v y
\\\\|________________ |
\\\\| |_______________V
\\\\| 1.5*I _______I_______|
\\\\|________________|
\\\\| :
\\\\|----------------|---------------|
2.0 m 2.0 m
>>> from sympy.physics.continuum_mechanics.beam import Beam
>>> from sympy import symbols
>>> E, I = symbols('E, I')
>>> R1, R2 = symbols('R1, R2')
>>> b1 = Beam(2, E, 1.5*I)
>>> b2 = Beam(2, E, I)
>>> b = b1.join(b2, "fixed")
>>> b.apply_load(20, 4, -1)
>>> b.apply_load(R1, 0, -1)
>>> b.apply_load(R2, 0, -2)
>>> b.bc_slope = [(0, 0)]
>>> b.bc_deflection = [(0, 0)]
>>> b.solve_for_reaction_loads(R1, R2)
>>> b.load
-2 -1 -1
80⋅<x> - 20⋅<x> + 20⋅<x - 4>
>>> b.shear_force()
-1 0 0
80⋅<x> - 20⋅<x> + 20⋅<x - 4>
>>> b.bending_moment()
0 1 1
80⋅<x> - 20⋅<x> + 20⋅<x - 4>
>>> b.slope()
⎛ 1 2 2 ⎞
⎜80⋅<x> - 10⋅<x> + 10⋅<x - 4> 120 ⎟
⎜─────────────────────────────── - ─── ⎟ ⎛ 1 2 2⎞ 0 ⎛ 1 2 2⎞ 0
⎜ I I 80.0⎟ 0 0.666666666666667⋅⎝80⋅<x> - 10⋅<x> + 10⋅<x - 4> ⎠⋅<x> 0.666666666666667⋅⎝80⋅<x> - 10⋅<x> + 10⋅<x - 4> ⎠⋅<x - 2>
⎜───────────────────────────────────── + ────⎟⋅<x - 2> + ──────────────────────────────────────────────────────── - ────────────────────────────────────────────────────────────
⎝ E E⋅I ⎠ E⋅I E⋅I
Example 10¶
A combined beam, with constant flexural rigidity E*I, is formed by joining
a Beam of length 2*l to the right of another Beam of length l. The whole beam
is fixed at both of its both end. A point load of magnitude P is also applied
from the top at a distance of 2*l from starting point.
---> x
|
\\\\| P v y |\\\\
\\\\| | |\\\\
\\\\| V |\\\\
\\\\|____________ ________________________|\\\\
\\\\|____________O________________________|\\\\
\\\\| : : |\\\\
\\\\| : : |\\\\
\\\\|------------|------------|-----------|\\\\
l l l
>>> from sympy.physics.continuum_mechanics.beam import Beam
>>> from sympy import symbols
>>> E, I = symbols('E, I')
>>> l = symbols('l', positive=True)
>>> b1 = Beam(l ,E,I)
>>> b2 = Beam(2*l ,E,I)
>>> b = b1.join(b2,"hinge")
>>> M1, A1, M2, A2, P = symbols('M1 A1 M2 A2 P')
>>> b.apply_load(A1, 0, -1)
>>> b.apply_load(M1, 0 ,-2)
>>> b.apply_load(P, 2*l, -1)
>>> b.apply_load(A2, 3*l, -1)
>>> b.apply_load(M2, 3*l, -2)
>>> b.bc_slope=[(0, 0), (3*l, 0)]
>>> b.bc_deflection=[(0, 0), (3*l, 0)]
>>> b.solve_for_reaction_loads(M1, A1, M2, A2)
>>> b.reaction_loads
⎧ -5⋅P -13⋅P 5⋅P⋅l -4⋅P⋅l ⎫
⎨A₁: ─────, A₂: ──────, M₁: ─────, M₂: ───────⎬
⎩ 18 18 18 9 ⎭
>>> b.load
-2 -2 -1 -1
5⋅P⋅l⋅<x> 4⋅P⋅l⋅<-3⋅l + x> 5⋅P⋅<x> -1 13⋅P⋅<-3⋅l + x>
─────────── - ────────────────── - ───────── + P⋅<-2⋅l + x> - ─────────────────
18 9 18 18
>>> b.shear_force()
-1 -1 0 0
5⋅P⋅l⋅<x> 4⋅P⋅l⋅<-3⋅l + x> 5⋅P⋅<x> 0 13⋅P⋅<-3⋅l + x>
─────────── - ────────────────── - ──────── + P⋅<-2⋅l + x> - ────────────────
18 9 18 18
>>> b.bending_moment()
0 0 1 1
5⋅P⋅l⋅<x> 4⋅P⋅l⋅<-3⋅l + x> 5⋅P⋅<x> 1 13⋅P⋅<-3⋅l + x>
────────── - ───────────────── - ──────── + P⋅<-2⋅l + x> - ────────────────
18 9 18 18
>>> b.slope()
⎛ 1 2 2⎞ ⎛ 1 2 2⎞ ⎛ 2 1 2 2 2⎞
⎜5⋅P⋅l⋅<x> 5⋅P⋅<x> 5⋅P⋅<-l + x> ⎟ 0 ⎜5⋅P⋅l⋅<x> 5⋅P⋅<x> 5⋅P⋅<-l + x> ⎟ 0 ⎜P⋅l 4⋅P⋅l⋅<-3⋅l + x> 5⋅P⋅<-l + x> P⋅<-2⋅l + x> 13⋅P⋅<-3⋅l + x> ⎟ 0
⎜────────── - ──────── + ─────────────⎟⋅<x> ⎜────────── - ──────── + ─────────────⎟⋅<-l + x> ⎜──── - ───────────────── - ───────────── + ───────────── - ────────────────⎟⋅<-l + x>
⎝ 18 36 36 ⎠ ⎝ 18 36 36 ⎠ ⎝ 18 9 36 2 36 ⎠
──────────────────────────────────────────── - ───────────────────────────────────────────────── + ───────────────────────────────────────────────────────────────────────────────────────
E⋅I E⋅I E⋅I
>>> b.deflection()
⎛ 2 3 3⎞ ⎛ 2 3 3⎞ ⎛ 3 2 2 3 3 3⎞
⎜5⋅P⋅l⋅<x> 5⋅P⋅<x> 5⋅P⋅<-l + x> ⎟ 0 ⎜5⋅P⋅l⋅<x> 5⋅P⋅<x> 5⋅P⋅<-l + x> ⎟ 0 ⎜5⋅P⋅l P⋅l ⋅(-l + x) 2⋅P⋅l⋅<-3⋅l + x> 5⋅P⋅<-l + x> P⋅<-2⋅l + x> 13⋅P⋅<-3⋅l + x> ⎟ 0
⎜────────── - ──────── + ─────────────⎟⋅<x> ⎜────────── - ──────── + ─────────────⎟⋅<-l + x> ⎜────── + ───────────── - ───────────────── - ───────────── + ───────────── - ────────────────⎟⋅<-l + x>
⎝ 36 108 108 ⎠ ⎝ 36 108 108 ⎠ ⎝ 54 18 9 108 6 108 ⎠
──────────────────────────────────────────── - ───────────────────────────────────────────────── + ─────────────────────────────────────────────────────────────────────────────────────────────────────────
E⋅I E⋅I E⋅I
Example 11¶
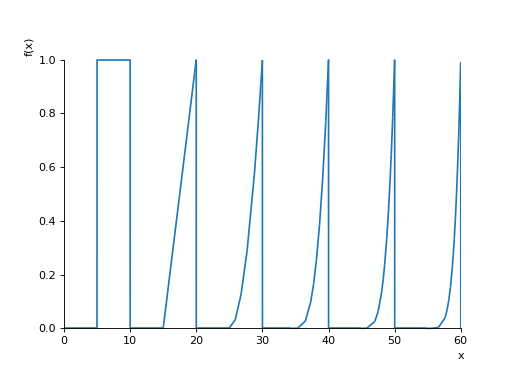
Any type of load defined by a polynomial can be applied to the beam. This allows approximation of arbitrary load distributions. The following example shows six truncated polynomial loads across the surface of a beam.
>>> n = 6
>>> b = Beam(10*n, E, I)
>>> for i in range(n):
... b.apply_load(1 / (5**i), 10*i + 5, i, end=10*i + 10)
>>> plot(b.load, (x, 0, 10*n)) # doctest: +SKIP