Cluster Analysis¶
Hierarchical Clustering¶
Hierarchical Clustering algorithm derived from the R package ‘amap’ [Amap].
The condensed distance matrix y can be computed by pdist() function in scipy (<http://docs.scipy.org/doc/scipy/reference/spatial.distance.html>)
- class mlpy.HCluster(method='complete')¶
Hierarchical Cluster.
Initialization.
Parameters : - method : string (‘ward’, ‘single’, ‘complete’, ‘average’, ‘mcquitty’, ‘median’, ‘centroid’)
the agglomeration method to be used
- cut(t)¶
Cuts the tree into several groups by specifying the cut height.
Parameters : - t : float
the threshold to apply when forming flat clusters
Returns : - clust : 1d numpy array
group memberships. Groups are in 0, ..., N-1.
- linkage(y)¶
Performs hierarchical clustering on the condensed distance matrix y.
Parameters : - y : 1d array_like object
condensed distance matrix y. y must be a C(n, 2) sized vector where n is the number of original observations paired in the distance matrix.
| [Amap] | amap: Another Multidimensional Analysis Package, http://cran.r-project.org/web/packages/amap/index.html |
Memory-saving Hierarchical Clustering¶
Memory-saving Hierarchical Clustering derived from the R and Python package ‘fastcluster’ [fastcluster].
- class mlpy.MFastHCluster(method='single')¶
Memory-saving Hierarchical Cluster (only euclidean distance).
This method needs O(NP) memory for clustering of N point in R^P.
Initialization.
Parameters : - method : string (‘single’, ‘centroid’, ‘median’, ‘ward’)
the agglomeration method to be used
- Z()¶
Returns the hierarchical clustering encoded as a linkage matrix. See scipy.cluster.hierarchy.linkage.
- cut(t)¶
Cuts the tree into several groups by specifying the cut height.
Parameters : - t : float
the threshold to apply when forming flat clusters
Returns : - clust : 1d numpy array
group memberships. Groups are in 0, ..., N-1.
- linkage(x)¶
Performs hierarchical clustering.
Parameters : - x : 2d array_like object (N, P)
vector data, N observations in R^P
| [fastcluster] | Fast hierarchical clustering routines for R and Python, http://cran.r-project.org/web/packages/fastcluster/index.html |
k-means¶
- mlpy.kmeans(x, k, plus=False, seed=0)¶
k-means clustering.
Parameters : - x : 2d array_like object (N, P)
data
- k : int (1<k<N)
number of clusters
- plus : bool
k-means++ algorithm for initialization
- seed : int
random seed for initialization
Returns : - clusters, means, steps: 1d array, 2d array, int
cluster membership in 0,...,K-1, means (K,P), number of steps
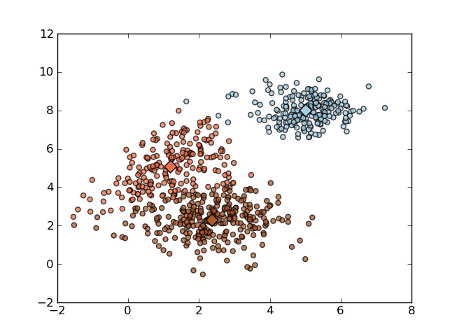
Example:
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> import mlpy
>>> np.random.seed(0)
>>> mean1, cov1, n1 = [1, 5], [[1,1],[1,2]], 200 # 200 points, mean=(1,5)
>>> x1 = np.random.multivariate_normal(mean1, cov1, n1)
>>> mean2, cov2, n2 = [2.5, 2.5], [[1,0],[0,1]], 300 # 300 points, mean=(2.5,2.5)
>>> x2 = np.random.multivariate_normal(mean2, cov2, n2)
>>> mean3, cov3, n3 = [5, 8], [[0.5,0],[0,0.5]], 200 # 200 points, mean=(5,8)
>>> x3 = np.random.multivariate_normal(mean3, cov3, n3)
>>> x = np.concatenate((x1, x2, x3), axis=0) # concatenate the samples
>>> cls, means, steps = mlpy.kmeans(x, k=3, plus=True)
>>> steps
13
>>> fig = plt.figure(1)
>>> plot1 = plt.scatter(x[:,0], x[:,1], c=cls, alpha=0.75)
>>> plot2 = plt.scatter(means[:,0], means[:,1], c=np.unique(cls), s=128, marker='d') # plot the means
>>> plt.show()