mlpy.wavelet - Wavelet Transform¶
Padding¶
- mlpy.wavelet.pad(x, method='reflection')¶
Pad to bring the total length N up to the next-higher power of two.
Parameters : - x : 1d array_like object
data
- method : string (‘reflection’, ‘periodic’, ‘zeros’)
method
Returns : - xp, orig : 1d numpy array, 1d numpy array bool
padded version of x and a boolean array with value True where xp contains the original data
Discrete Wavelet Transform¶
Discrete Wavelet Transform based on the GSL DWT [Gsldwt].
For the forward transform, the output is the discrete wavelet transform
 in a packed triangular storage layout, where
in a packed triangular storage layout, where  is the index of the level
is the index of the level 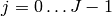 and
and  is the index
of the coefficient within each level,
is the index
of the coefficient within each level,  .
The total number of levels is
.
The total number of levels is 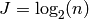 . The output data
has the following form,
. The output data
has the following form,
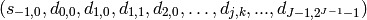
where the first element is the smoothing coefficient 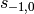 ,
followed by the detail coefficients
,
followed by the detail coefficients  for each level
for each level  .
The backward transform inverts these coefficients to obtain the original data.
.
The backward transform inverts these coefficients to obtain the original data.
Note
from GSL online manual (http://www.gnu.org/software/gsl/manual/)
- mlpy.wavelet.dwt(x, wf, k, centered=False)¶
Discrete Wavelet Tranform
Parameters : - x : 1d array_like object (the length is restricted to powers of two)
data
- wf : string (‘d’: daubechies, ‘h’: haar, ‘b’: bspline)
wavelet family
- k : integer
member of the wavelet family
- daubechies : k = 4, 6, ..., 20 with k even
- haar : the only valid choice of k is k = 2
- bspline : k = 103, 105, 202, 204, 206, 208, 301, 303, 305 307, 309
- centered : bool
align the coefficients of the various sub-bands on edges. Thus the resulting visualization of the coefficients of the wavelet transform in the phase plane is easier to understand.
Returns : - X : 1d numpy array
discrete wavelet transformed data
Example
>>> import numpy as np >>> import mlpy.wavelet as wave >>> x = np.array([1,2,3,4,3,2,1,0]) >>> wave.dwt(x=x, wf='d', k=6) array([ 5.65685425, 3.41458985, 0.29185347, -0.29185347, -0.28310081, -0.07045258, 0.28310081, 0.07045258])
- mlpy.wavelet.idwt(X, wf, k, centered=False)¶
Inverse Discrete Wavelet Tranform
Parameters : - X : 1d array_like object
discrete wavelet transformed data
- wf : string (‘d’: daubechies, ‘h’: haar, ‘b’: bspline)
wavelet type
- k : integer
member of the wavelet family
- daubechies : k = 4, 6, ..., 20 with k even
- haar : the only valid choice of k is k = 2
- bspline : k = 103, 105, 202, 204, 206, 208, 301, 303, 305 307, 309
- centered : bool
if the coefficients are aligned
Returns : - x : 1d numpy array
data
Example:
>>> import numpy as np >>> import mlpy.wavelet as wave >>> X = np.array([ 5.65685425, 3.41458985, 0.29185347, -0.29185347, -0.28310081, ... -0.07045258, 0.28310081, 0.07045258]) >>> wave.idwt(X=X, wf='d', k=6) array([ 1.00000000e+00, 2.00000000e+00, 3.00000000e+00, 4.00000000e+00, 3.00000000e+00, 2.00000000e+00, 1.00000000e+00, -3.53954610e-09])
Undecimated Wavelet Transform¶
Undecimated Wavelet Transform (also known as stationary wavelet transform, redundant wavelet transform, translation invariant wavelet transform, shift invariant wavelet transform or Maximal overlap wavelet transform) based on the “wavelets” R package.
- mlpy.wavelet.uwt(x, wf, k, levels=0)¶
Undecimated Wavelet Tranform
Parameters : - x : 1d array_like object (the length is restricted to powers of two)
data
- wf : string (‘d’: daubechies, ‘h’: haar, ‘b’: bspline)
wavelet family
- k : int
member of the wavelet family
- daubechies: k = 4, 6, ..., 20 with k even
- haar: the only valid choice of k is k = 2
- bspline: k = 103, 105, 202, 204, 206, 208, 301, 303, 305 307, 309
- levels : int
level of the decomposition (J). If levels = 0 this is the value J such that the length of X is at least as great as the length of the level J wavelet filter, but less than the length of the level J+1 wavelet filter. Thus, j <= log_2((n-1)/(l-1)+1), where n is the length of x
Returns : - X : 2d numpy array (2J * len(x))
misaligned scaling and wavelet coefficients:
[[wavelet coefficients W_1] [wavelet coefficients W_2] : [wavelet coefficients W_J] [scaling coefficients V_1] [scaling coefficients V_2] : [scaling coefficients V_J]]
- mlpy.wavelet.iuwt(X, wf, k)¶
Inverse Undecimated Wavelet Tranform
Parameters : - X : 2d array_like object (the length is restricted to powers of two)
misaligned scaling and wavelet coefficients
- wf : string (‘d’: daubechies, ‘h’: haar, ‘b’: bspline)
wavelet family
- k : int
member of the wavelet family
- daubechies: k = 4, 6, ..., 20 with k even
- haar: the only valid choice of k is k = 2
- bspline: k = 103, 105, 202, 204, 206, 208, 301, 303, 305 307, 309
Returns : - x : 1d numpy array
data
- mlpy.wavelet.uwt_align_h2(X, inverse=False)¶
UWT h2 coefficients aligment.
If inverse = True performs the misalignment for a correct reconstruction.
- mlpy.wavelet.uwt_align_d4(X, inverse=False)¶
UWT d4 coefficients aligment.
If inverse = True performs the misalignment for a correct reconstruction.
Continuous Wavelet Transform¶
Continuous Wavelet Transform based on [Torrence98].
- mlpy.wavelet.cwt(x, dt, scales, wf='dog', p=2)¶
Continuous Wavelet Tranform.
Parameters : - x : 1d array_like object
data
- dt : float
time step
- scales : 1d array_like object
scales
- wf : string (‘morlet’, ‘paul’, ‘dog’)
wavelet function
- p : float
wavelet function parameter (‘omega0’ for morlet, ‘m’ for paul and dog)
Returns : - X : 2d numpy array
transformed data
- mlpy.wavelet.icwt(X, dt, scales, wf='dog', p=2)¶
Inverse Continuous Wavelet Tranform. The reconstruction factor is not applied.
Parameters : - X : 2d array_like object
transformed data
- dt : float
time step
- scales : 1d array_like object
scales
- wf : string (‘morlet’, ‘paul’, ‘dog’)
wavelet function
- p : float
wavelet function parameter
Returns : - x : 1d numpy array
data
- mlpy.wavelet.autoscales(N, dt, dj, wf, p)¶
Compute scales as fractional power of two.
Parameters : - N : integer
number of data samples
- dt : float
time step
- dj : float
scale resolution (smaller values of dj give finer resolution)
- wf : string
wavelet function (‘morlet’, ‘paul’, ‘dog’)
- p : float
omega0 (‘morlet’) or order (‘paul’, ‘dog’)
Returns : - scales : 1d numpy array
scales
- mlpy.wavelet.fourier_from_scales(scales, wf, p)¶
Compute the equivalent fourier period from scales.
Parameters : - scales : list or 1d numpy array
scales
- wf : string (‘morlet’, ‘paul’, ‘dog’)
wavelet function
- p : float
wavelet function parameter (‘omega0’ for morlet, ‘m’ for paul and dog)
Returns : fourier wavelengths
- mlpy.wavelet.scales_from_fourier(f, wf, p)¶
Compute scales from fourier period.
Parameters : - f : list or 1d numpy array
fourier wavelengths
- wf : string (‘morlet’, ‘paul’, ‘dog’)
wavelet function
- p : float
wavelet function parameter (‘omega0’ for morlet, ‘m’ for paul and dog)
Returns : scales
| [Torrence98] | C Torrence and G P Compo. Practical Guide to Wavelet Analysis |
| [Gsldwt] | Gnu Scientific Library, http://www.gnu.org/software/gsl/ |
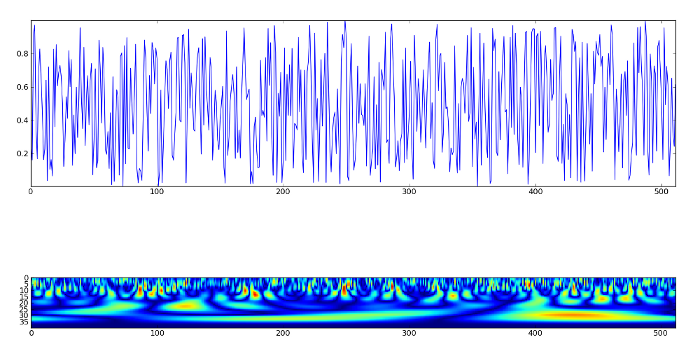
Example (requires matplotlib)
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> import mlpy.wavelet as wave
>>> x = np.random.sample(512)
>>> scales = wave.autoscales(N=x.shape[0], dt=1, dj=0.25, wf='dog', p=2)
>>> X = wave.cwt(x=x, dt=1, scales=scales, wf='dog', p=2)
>>> fig = plt.figure(1)
>>> ax1 = plt.subplot(2,1,1)
>>> p1 = ax1.plot(x)
>>> ax1.autoscale_view(tight=True)
>>> ax2 = plt.subplot(2,1,2)
>>> p2 = ax2.imshow(np.abs(X), interpolation='nearest')
>>> plt.show()