Internal documentation of the scan op

Top-level description of scan

The scan operation is meant to be able to describe symbolically loops, recurrent relations or dynamical systems. In general, we will say that the scan op implements system of equations of the following form:

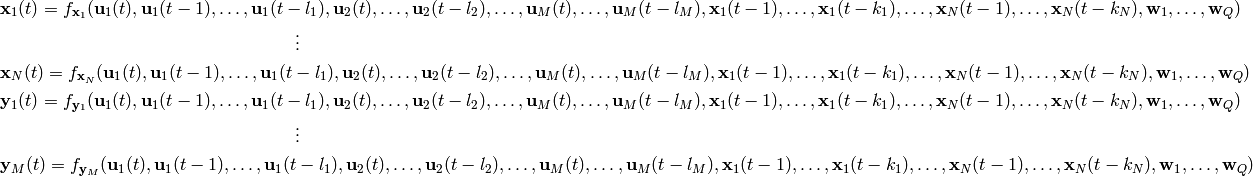
\mathbf{x}_1(t) = f_{\mathbf{x}_1} (\mathbf{u}_1(t), \mathbf{u}_1(t-1), \ldots, \mathbf{u}_1(t-l_1), \mathbf{u}_2(t), \ldots, \mathbf{u}_2(t-l_2), \ldots, \mathbf{u}_M(t), \ldots, \mathbf{u}_M(t - l_M), \mathbf{x}_1(t-1), \ldots, \mathbf{x}_1(t-k_1), \ldots, \mathbf{x}_N(t-1), \ldots, \mathbf{x}_N(t-k_N), \mathbf{w}_1, \ldots, \mathbf{w}_Q) \vdots \mathbf{x}_N(t) = f_{\mathbf{x}_N} (\mathbf{u}_1(t), \mathbf{u}_1(t-1), \ldots, \mathbf{u}_1(t-l_1), \mathbf{u}_2(t), \ldots, \mathbf{u}_2(t-l_2), \ldots, \mathbf{u}_M(t), \ldots, \mathbf{u}_M(t - l_M), \mathbf{x}_1(t-1), \ldots, \mathbf{x}_1(t-k_1), \ldots, \mathbf{x}_N(t-1), \ldots, \mathbf{x}_N(t-k_N), \mathbf{w}_1, \ldots, \mathbf{w}_Q) \mathbf{y}_1(t) = f_{\mathbf{y}_1} (\mathbf{u}_1(t), \mathbf{u}_1(t-1), \ldots, \mathbf{u}_1(t-l_1), \mathbf{u}_2(t), \ldots, \mathbf{u}_2(t-l_2), \ldots, \mathbf{u}_M(t), \ldots, \mathbf{u}_M(t - l_M), \mathbf{x}_1(t-1), \ldots, \mathbf{x}_1(t-k_1), \ldots, \mathbf{x}_N(t-1), \ldots, \mathbf{x}_N(t-k_N), \mathbf{w}_1, \ldots, \mathbf{w}_Q) \vdots \mathbf{y}_M(t) = f_{\mathbf{y}_M} (\mathbf{u}_1(t), \mathbf{u}_1(t-1), \ldots, \mathbf{u}_1(t-l_1), \mathbf{u}_2(t), \ldots, \mathbf{u}_2(t-l_2), \ldots, \mathbf{u}_M(t), \ldots, \mathbf{u}_M(t - l_M), \mathbf{x}_1(t-1), \ldots, \mathbf{x}_1(t-k_1), \ldots, \mathbf{x}_N(t-1), \ldots, \mathbf{x}_N(t-k_N), \mathbf{w}_1, \ldots, \mathbf{w}_Q)

The equations describe a system evolving in time, where 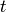t represents the current step. The system is described by inputs, states, outputs and parameteres.

The inputs, denoted by 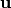\mathbf{u} are time-varying quantities, hence indexed by 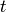t. They however only influence the system, but are not influenced by the system.

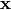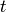The states \mathbf{x} are time-varying quantities, whose value at time t depends on its (or other state) previous values as well as the inputs and parameters. Note that the first few values of the states are always provided, otherwise we could not imploy the recurrent equation to generate these sequence of values without a starting point.

The outputs, 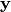\mathbf{y} are outputs of the system, i.e. values that depend on the previous values of the states and inputs. The difference between outputs and states is that outputs do not feed back into the system.

The parameters 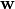\mathbf{w} are fixed quantities that are re-used at every time step of the evolution of the system.

Each of the equations above are implemented by the inner function of scan. You can think of the inner function as a theano function that gets executed at each step to get the new values. This inner function should not be confused with the constructive function, which is what the user gives to the scan function. The constructive function is used to construct the computational graph that is afterwards compiled into the inner function.

Naming conventions

  • input_state will stand for a state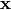 \mathbf{x}, when it is provided as an input to the recurrent formula (the inner function) that will generate the new value of the state
  • output_state will stand for a state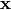 \mathbf{x} when it refers to the result of the recurrent formula (the output of the inner function)
  • output will stand for an output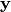 \mathbf{y}
  • input will be an input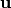 \mathbf{u}
  • parameter will stand for a parameter tensor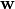 \mathbf{w} that stays constant at each step of the inner function
  • non_numeric_input_state will stand for states that are not numeric in nature, more specifically random states, when they are provided as an input. The same holds for non_numeric_output_state.
  • t is the time index (the current step in the evolution of the system).
  • T is the total number of steps in the evolution of the system.
  • the suffix _slices added to either x or u will mean the list of variables representing slices of states or inputs. These are the arguments given to the constructive function of scan (see above).
  • the suffix _inner added to x, y, xy, u, w or z will mean the variables representing the state/output/input/weights in the inner function
  • the suffix _outer added to x, y, xy, u, w or z will mean the variables representing the state/output/input/weights in the main computational graph (the one containing the scan op).

Files

The implementation of scan is spread over several files. The different files, and section of the code they deal with, are :

  • scan.py implements the scan function. The scan function arranges the arguments of scan correctly, constructs the scan op and afterwards calls the constructed scan op on the arguments. This function takes care of figuring out missing inputs and shared variables.
  • scan_op.py implements the scanOp class. The scanOp respects the Op interface, and contains most of the logic of the scan operator.
  • scan_utils.py contains several helpful functions used through out the other files that are specific of the scan operator.
  • scan_views.py contains different views of the scan op that have simpler and easier signatures to be used in specific cases.
  • scan_opt.py contains the list of all optimizations for the scan operator.

The logical flow

First the scan arguments are parsed by the function canonical_arguments, that wraps them into lists and adds default values for the arguments. One important step that happens in this function is that the inputs arguments are converted such that they all have a single tap, namely 0. For example if you have [{'input':u, 'taps':[0, 4]}] as the list of inputs arguments to scan, it gets converted into [{'input':u, 'taps':[0]}, {'input':u[4:], 'taps':[0]}].

The second step is to check if n_steps is a constant and has the value 1 or -1. If that is true then the function one_step_scan is called which unwraps the computation of the inner function into the outer graph without adding any scan op in the graph.