Graph optimization¶

In this section we will define a couple optimizations on doubles.

Todo

This tutorial goes way too far under the hood, for someone who just wants to add yet another pattern to the libraries in tensor.opt for example.

We need another tutorial that covers the decorator syntax, and explains how to register your optimization right away. That’s what you need to get going.

Later, the rest is more useful for when that decorator syntax type thing doesn’t work. (There are optimizations that don’t fit that model).

Note

The optimization tag cxx_only is used for optimizations that insert Ops which have no Python implementation (so they only have C code). Optimizations with this tag are skipped when there is no C++ compiler available.

Global and local optimizations¶

First, let’s lay out the way optimizations work in Theano. There are two types of optimizations: global optimizations and local optimizations. A global optimization takes a FunctionGraph object (a FunctionGraph is a wrapper around a whole computation graph, you can see its documentation for more details) and navigates through it in a suitable way, replacing some Variables by others in the process. A local optimization, on the other hand, is defined as a function on a single Apply node and must return either False (to mean that nothing is to be done) or a list of new Variables that we would like to replace the node’s outputs with. A Navigator is a special kind of global optimization which navigates the computation graph in some fashion (in topological order, reverse-topological order, random order, etc.) and applies one or more local optimizations at each step.

Optimizations which are holistic, meaning that they must take into account dependencies that might be all over the graph, should be global. Optimizations that can be done with a narrow perspective are better defined as local optimizations. The majority of optimizations we want to define are local.

Global optimization¶

A global optimization (or optimizer) is an object which defines the following methods:

class Optimizer¶

apply(fgraph)¶: This method takes a FunctionGraph object which contains the computation graph and does modifications in line with what the optimization is meant to do. This is one of the main methods of the optimizer.

add_requirements(fgraph)¶: This method takes a FunctionGraph object and adds features to it. These features are “plugins” that are needed for the apply method to do its job properly.

optimize(fgraph)¶

This is the interface function called by Theano.

Default: this is defined by Optimizer as add_requirement(fgraph); apply(fgraph).

See the section about FunctionGraph to understand how to define these methods.

Local optimization¶

A local optimization is an object which defines the following methods:

class LocalOptimizer¶

transform(node)¶: This method takes an Apply node and returns either False to signify that no changes are to be done or a list of Variables which matches the length of the node’s outputs list. When the LocalOptimizer is applied by a Navigator, the outputs of the node passed as argument to the LocalOptimizer will be replaced by the list returned.

One simplification rule¶

For starters, let’s define the following simplification:

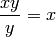
$\frac{xy}{y} = x$

We will implement it in three ways: using a global optimization, a local optimization with a Navigator and then using the PatternSub facility.

Global optimization¶

Here is the code for a global optimization implementing the simplification described above:

import theano
from theano import gof
from theano.gof import toolbox

class Simplify(gof.Optimizer):
    def add_requirements(self, fgraph):
        fgraph.attach_feature(toolbox.ReplaceValidate())
    def apply(self, fgraph):
        for node in fgraph.toposort():
            if node.op == true_div:
                x, y = node.inputs
                z = node.outputs[0]
                if x.owner and x.owner.op == mul:
                    a, b = x.owner.inputs
                    if y == a:
                        fgraph.replace_validate(z, b)
                    elif y == b:
                        fgraph.replace_validate(z, a)

simplify = Simplify()

Todo

What is add_requirements? Why would we know to do this? Are there other requirements we might want to know about?

Here’s how it works: first, in add_requirements, we add the ReplaceValidate FunctionGraph Features located in toolbox – [doc TODO]. This feature adds the replace_validate method to fgraph, which is an enhanced version of replace that does additional checks to ensure that we are not messing up the computation graph (note: if ReplaceValidate was already added by another optimizer, extend will do nothing). In a nutshell, toolbox.ReplaceValidate grants access to fgraph.replace_validate, and fgraph.replace_validate allows us to replace a Variable with another while respecting certain validation constraints. You can browse the list of FunctionGraph Feature List and see if some of them might be useful to write optimizations with. For example, as an exercise, try to rewrite Simplify using NodeFinder. (Hint: you want to use the method it publishes instead of the call to toposort!)

Then, in apply we do the actual job of simplification. We start by iterating through the graph in topological order. For each node encountered, we check if it’s a div node. If not, we have nothing to do here. If so, we put in x, y and z the numerator, denominator and quotient (output) of the division. The simplification only occurs when the numerator is a multiplication, so we check for that. If the numerator is a multiplication we put the two operands in a and b, so we can now say that z == (a*b)/y. If y==a then z==b and if y==b then z==a. When either case happens then we can replace z by either a or b using fgraph.replace_validate - else we do nothing. You might want to check the documentation about Variable and Apply to get a better understanding of the pointer-following game you need to get ahold of the nodes of interest for the simplification (x, y, z, a, b, etc.).

Test time:

>>> from theano.scalar import float64, add, mul, true_div
>>> x = float64('x')
>>> y = float64('y')
>>> z = float64('z')
>>> a = add(z, mul(true_div(mul(y, x), y), true_div(z, x)))
>>> e = gof.FunctionGraph([x, y, z], [a])
>>> e
[add(z, mul(true_div(mul(y, x), y), true_div(z, x)))]
>>> simplify.optimize(e)
>>> e
[add(z, mul(x, true_div(z, x)))]

Cool! It seems to work. You can check what happens if you put many instances of $\frac{xy}{y}$ in the graph. Note that it sometimes won’t work for reasons that have nothing to do with the quality of the optimization you wrote. For example, consider the following:

>>> x = float64('x')
>>> y = float64('y')
>>> z = float64('z')
>>> a = true_div(mul(add(y, z), x), add(y, z))
>>> e = gof.FunctionGraph([x, y, z], [a])
>>> e
[true_div(mul(add(y, z), x), add(y, z))]
>>> simplify.optimize(e)
>>> e
[true_div(mul(add(y, z), x), add(y, z))]

Nothing happened here. The reason is: add(y, z) != add(y, z). That is the case for efficiency reasons. To fix this problem we first need to merge the parts of the graph that represent the same computation, using the MergeOptimizer defined in theano.gof.opt.

>>> from theano.gof.opt import MergeOptimizer
>>> MergeOptimizer().optimize(e)  
(0, ..., None, None, {}, 1, 0)
>>> e
[true_div(mul(*1 -> add(y, z), x), *1)]
>>> simplify.optimize(e)
>>> e
[x]

Once the merge is done, both occurrences of add(y, z) are collapsed into a single one and is used as an input in two places. Note that add(x, y) and add(y, x) are still considered to be different because Theano has no clue that add is commutative. You may write your own global optimizer to identify computations that are identical with full knowledge of the rules of arithmetics that your Ops implement. Theano might provide facilities for this somewhere in the future.

Note

FunctionGraph is a Theano structure intended for the optimization phase. It is used internally by function and is rarely exposed to the end user. You can use it to test out optimizations, etc. if you are comfortable with it, but it is recommended to use the function frontend and to interface optimizations with optdb (we’ll see how to do that soon).

Local optimization¶

The local version of the above code would be the following:

class LocalSimplify(gof.LocalOptimizer):
    def transform(self, node):
        if node.op == true_div:
            x, y = node.inputs
            if x.owner and x.owner.op == mul:
                a, b = x.owner.inputs
                if y == a:
                    return [b]
                elif y == b:
                    return [a]
        return False
    def tracks(self):
        # This should be needed for the EquilibriumOptimizer
        # but it isn't now
        # TODO: do this and explain it
        return [] # that's not what you should do

local_simplify = LocalSimplify()

Todo

Fix up previous example... it’s bad and incomplete.

The definition of transform is the inner loop of the global optimizer, where the node is given as argument. If no changes are to be made, False must be returned. Else, a list of what to replace the node’s outputs with must be returned. This list must have the same length as node.ouputs. If one of node.outputs don’t have clients(it is not used in the graph), you can put None in the returned list to remove it.

In order to apply the local optimizer we must use it in conjunction with a Navigator. Basically, a Navigator is a global optimizer that loops through all nodes in the graph (or a well-defined subset of them) and applies one or several local optimizers on them.

>>> x = float64('x')
>>> y = float64('y')
>>> z = float64('z')
>>> a = add(z, mul(true_div(mul(y, x), y), true_div(z, x)))
>>> e = gof.FunctionGraph([x, y, z], [a])
>>> e
[add(z, mul(true_div(mul(y, x), y), true_div(z, x)))]
>>> simplify = gof.TopoOptimizer(local_simplify)
>>> simplify.optimize(e)
(<theano.gof.opt.TopoOptimizer object at 0x...>, 1, 5, 3, ..., ..., ...)
>>> e
[add(z, mul(x, true_div(z, x)))]

OpSub, OpRemove, PatternSub¶

Theano defines some shortcuts to make LocalOptimizers:

OpSub(op1, op2)¶: Replaces all uses of op1 by op2. In other words, the outputs of all Apply involving op1 by the outputs of Apply nodes involving op2, where their inputs are the same.

OpRemove(op)¶: Removes all uses of op in the following way: if y = op(x) then y is replaced by x. op must have as many outputs as it has inputs. The first output becomes the first input, the second output becomes the second input, and so on.

PatternSub(pattern1, pattern2)¶: Replaces all occurrences of the first pattern by the second pattern. See PatternSub.

from theano.gof.opt import OpSub, OpRemove, PatternSub

# Replacing add by mul (this is not recommended for primarily
# mathematical reasons):
add_to_mul = OpSub(add, mul)

# Removing identity
remove_identity = OpRemove(identity)

# The "simplify" operation we've been defining in the past few
# sections. Note that we need two patterns to account for the
# permutations of the arguments to mul.
local_simplify_1 = PatternSub((true_div, (mul, 'x', 'y'), 'y'),
                              'x')
local_simplify_2 = PatternSub((true_div, (mul, 'x', 'y'), 'x'),
                              'y')

Note

OpSub, OpRemove and PatternSub produce local optimizers, which means that everything we said previously about local optimizers apply: they need to be wrapped in a Navigator, etc.

Todo

wtf is a navigator?

When an optimization can be naturally expressed using OpSub, OpRemove or PatternSub, it is highly recommended to use them.

WRITEME: more about using PatternSub (syntax for the patterns, how to use constraints, etc. - there’s some decent doc at PatternSub for those interested)

The optimization database (optdb)¶

Theano exports a symbol called optdb which acts as a sort of ordered database of optimizations. When you make a new optimization, you must insert it at the proper place in the database. Furthermore, you can give each optimization in the database a set of tags that can serve as a basis for filtering.

The point of optdb is that you might want to apply many optimizations to a computation graph in many unique patterns. For example, you might want to do optimization X, then optimization Y, then optimization Z. And then maybe optimization Y is an EquilibriumOptimizer containing LocalOptimizers A, B and C which are applied on every node of the graph until they all fail to change it. If some optimizations act up, we want an easy way to turn them off. Ditto if some optimizations are very CPU-intensive and we don’t want to take the time to apply them.

The optdb system allows us to tag each optimization with a unique name as well as informative tags such as ‘stable’, ‘buggy’ or ‘cpu_intensive’, all this without compromising the structure of the optimizations.

Definition of optdb¶

optdb is an object which is an instance of SequenceDB, itself a subclass of DB. There exist (for now) two types of DB, SequenceDB and EquilibriumDB. When given an appropriate Query, DB objects build an Optimizer matching the query.

A SequenceDB contains Optimizer or DB objects. Each of them has a name, an arbitrary number of tags and an integer representing their order in the sequence. When a Query is applied to a SequenceDB, all Optimizers whose tags match the query are inserted in proper order in a SequenceOptimizer, which is returned. If the SequenceDB contains DB instances, the Query will be passed to them as well and the optimizers they return will be put in their places.

An EquilibriumDB contains LocalOptimizer or DB objects. Each of them has a name and an arbitrary number of tags. When a Query is applied to an EquilibriumDB, all LocalOptimizers that match the query are inserted into an EquilibriumOptimizer, which is returned. If the SequenceDB contains DB instances, the Query will be passed to them as well and the LocalOptimizers they return will be put in their places (note that as of yet no DB can produce LocalOptimizer objects, so this is a moot point).

Theano contains one principal DB object, optdb, which contains all of Theano’s optimizers with proper tags. It is recommended to insert new Optimizers in it. As mentioned previously, optdb is a SequenceDB, so, at the top level, Theano applies a sequence of global optimizations to the computation graphs.

Query¶

A Query is built by the following call:

theano.gof.Query(include, require=None, exclude=None, subquery=None)

class Query¶

include¶: A set of tags (a tag being a string) such that every optimization obtained through this Query must have one of the tags listed. This field is required and basically acts as a starting point for the search.

require¶: A set of tags such that every optimization obtained through this Query must have all of these tags.

exclude¶: A set of tags such that every optimization obtained through this Query must have none of these tags.

subquery¶: optdb can contain sub-databases; subquery is a dictionary mapping the name of a sub-database to a special Query. If no subquery is given for a sub-database, the original Query will be used again.

Furthermore, a Query object includes three methods, including, requiring and excluding which each produce a new Query object with include, require and exclude sets refined to contain the new [WRITEME]

Examples¶

Here are a few examples of how to use a Query on optdb to produce an Optimizer:

from theano.gof import Query
from theano.compile import optdb

# This is how the optimizer for the fast_run mode is defined
fast_run = optdb.query(Query(include=['fast_run']))

# This is how the optimizer for the fast_compile mode is defined
fast_compile = optdb.query(Query(include=['fast_compile']))

# This is the same as fast_run but no optimizations will replace
# any operation by an inplace version. This assumes, of course,
# that all inplace operations are tagged as 'inplace' (as they
# should!)
fast_run_no_inplace = optdb.query(Query(include=['fast_run'],
                                        exclude=['inplace']))

Registering an Optimizer¶

Let’s say we have a global optimizer called simplify. We can add it to optdb as follows:

# optdb.register(name, optimizer, order, *tags)
optdb.register('simplify', simplify, 0.5, 'fast_run')

Once this is done, the FAST_RUN mode will automatically include your optimization (since you gave it the ‘fast_run’ tag). Of course, already-compiled functions will see no change. The ‘order’ parameter (what it means and how to choose it) will be explained in optdb structure below.

Registering a LocalOptimizer¶

LocalOptimizers may be registered in two ways:

Wrap them in a Navigator and insert them like a global optimizer (see previous section).
Put them in an EquilibriumDB.

Theano defines two EquilibriumDBs where you can put local optimizations:

canonicalize()¶

This contains optimizations that aim to simplify the graph:

Replace rare or esoterical operations with their equivalents using elementary operations.
Order operations in a canonical way (any sequence of multiplications and divisions can be rewritten to contain at most one division, for example; x*x can be rewritten x**2; etc.)
Fold constants (Constant(2)*Constant(2) becomes Constant(4))

specialize()¶

This contains optimizations that aim to specialize the graph:

Replace a combination of operations with a special operation that does the same thing (but better).

For each group, all optimizations of the group that are selected by the Query will be applied on the graph over and over again until none of them is applicable, so keep that in mind when designing it: check carefully that your optimization leads to a fixpoint (a point where it cannot apply anymore) at which point it returns False to indicate its job is done. Also be careful not to undo the work of another local optimizer in the group, because then the graph will oscillate between two or more states and nothing will get done.

optdb structure¶

optdb contains the following Optimizers and sub-DBs, with the given priorities and tags:

Order	Name	Description
0	merge1	First merge operation
1	canonicalize	Simplify the graph
2	specialize	Add specialized operations
49	merge2	Second merge operation
49.5	add_destroy_handler	Enable inplace optimizations
100	merge3	Third merge operation

The merge operations are meant to put together parts of the graph that represent the same computation. Since optimizations can modify the graph in such a way that two previously different-looking parts of the graph become similar, we merge at the beginning, in the middle and at the very end. Technically, we only really need to do it at the end, but doing it in previous steps reduces the size of the graph and therefore increases the efficiency of the process.

See previous section for more information about the canonicalize and specialize steps.

The add_destroy_handler step is not really an optimization. It is a marker. Basically:

Warning

Any optimization which inserts inplace operations in the computation graph must appear after the add_destroy_handler “optimizer”. In other words, the priority of any such optimization must be >= 50. Failure to comply by this restriction can lead to the creation of incorrect computation graphs.

The reason the destroy handler is not inserted at the beginning is that it is costly to run. It is cheaper to run most optimizations under the assumption there are no inplace operations.

Navigator¶

WRITEME

Profiling Theano function compilation¶

You find that compiling a Theano function is taking too much time? You can get profiling information about Theano optimization. The normal Theano profiler will provide you with very high-level information. The indentation shows the included in/subset relationship between sections. The top of its output look like this:

Function profiling
==================
  Message: PATH_TO_A_FILE:23
  Time in 0 calls to Function.__call__: 0.000000e+00s
  Total compile time: 1.131874e+01s
    Number of Apply nodes: 50
    Theano Optimizer time: 1.152431e+00s
       Theano validate time: 2.790451e-02s
    Theano Linker time (includes C, CUDA code generation/compiling): 7.893991e-02s
       Import time 1.153541e-02s
  Time in all call to theano.grad() 4.732513e-02s

Explanations:

Total compile time: 1.131874e+01s gives the total time spent inside theano.function.
Number of Apply nodes: 50 means that after optimization, there are 50 apply node in the graph.
Theano Optimizer time: 1.152431e+00s means that we spend 1.15s in the theano.function phase where we optimize (modify) the graph to make it faster / more stable numerically / work on GPU /...
Theano validate time: 2.790451e-02s means that we spent 2.8e-2s in the validate subset of the optimization phase.
Theano Linker time (includes C, CUDA code generation/compiling): 7.893991e-02s means that we spent 7.9e-2s in linker phase of theano.function.
Import time 1.153541e-02s is a subset of the linker time where we import the compiled module.
Time in all call to theano.grad() 4.732513e-02s tells that we spent a total of 4.7e-2s in all calls to theano.grad. This is outside of the calls to theano.function.

The linker phase includes the generation of the C code, the time spent by g++ to compile and the time needed by Theano to build the object we return. The C code generation and compilation is cached, so the first time you compile a function and the following ones could take different amount of execution time.

Detailed profiling of Theano optimizer¶

You can get more detailed profiling information about the Theano optimizer phase by setting to True the Theano flags config.profile_optimizer (this require config.profile to be True as well).

This will output something like this:

Optimizer Profile
-----------------
 SeqOptimizer  OPT_FAST_RUN  time 1.152s for 123/50 nodes before/after optimization
   0.028s for fgraph.validate()
   0.131s for callback
   time      - (name, class, index) - validate time
   0.751816s - ('canonicalize', 'EquilibriumOptimizer', 4) - 0.004s
     EquilibriumOptimizer      canonicalize
       time 0.751s for 14 passes
       nb nodes (start, end,  max) 108 81 117
       time io_toposort 0.029s
       time in local optimizers 0.687s
       time in global optimizers 0.010s
        0 - 0.050s 27 (0.000s in global opts, 0.002s io_toposort) - 108 nodes - ('local_dimshuffle_lift', 9) ('local_upcast_elemwise_constant_inputs', 5) ('local_shape_to_shape_i', 3) ('local_fill_sink', 3) ('local_fill_to_alloc', 2) ...
        1 - 0.288s 26 (0.002s in global opts, 0.002s io_toposort) - 117 nodes - ('local_dimshuffle_lift', 8) ('local_fill_sink', 4) ('constant_folding', 4) ('local_useless_elemwise', 3) ('local_subtensor_make_vector', 3) ...
        2 - 0.044s 13 (0.002s in global opts, 0.003s io_toposort) - 96 nodes - ('constant_folding', 4) ('local_dimshuffle_lift', 3) ('local_fill_sink', 3) ('local_useless_elemwise', 1) ('local_fill_to_alloc', 1) ...
        3 - 0.045s 11 (0.000s in global opts, 0.002s io_toposort) - 91 nodes - ('constant_folding', 3) ('local_fill_to_alloc', 2) ('local_dimshuffle_lift', 2) ('local_mul_canonizer', 2) ('MergeOptimizer', 1) ...
        4 - 0.035s 8 (0.002s in global opts, 0.002s io_toposort) - 93 nodes - ('local_fill_sink', 3) ('local_dimshuffle_lift', 2) ('local_fill_to_alloc', 1) ('MergeOptimizer', 1) ('constant_folding', 1)
        5 - 0.035s 6 (0.000s in global opts, 0.002s io_toposort) - 88 nodes - ('local_fill_sink', 2) ('local_dimshuffle_lift', 2) ('local_fill_to_alloc', 1) ('local_mul_canonizer', 1)
        6 - 0.038s 10 (0.001s in global opts, 0.002s io_toposort) - 95 nodes - ('local_fill_sink', 3) ('local_dimshuffle_lift', 3) ('constant_folding', 2) ('local_fill_to_alloc', 1) ('MergeOptimizer', 1)
        7 - 0.032s 5 (0.001s in global opts, 0.002s io_toposort) - 91 nodes - ('local_fill_sink', 3) ('MergeOptimizer', 1) ('local_dimshuffle_lift', 1)
        8 - 0.034s 5 (0.000s in global opts, 0.002s io_toposort) - 92 nodes - ('local_fill_sink', 3) ('MergeOptimizer', 1) ('local_greedy_distributor', 1)
        9 - 0.031s 6 (0.001s in global opts, 0.002s io_toposort) - 90 nodes - ('local_fill_sink', 2) ('local_fill_to_alloc', 1) ('MergeOptimizer', 1) ('local_dimshuffle_lift', 1) ('local_greedy_distributor', 1)
       10 - 0.032s 5 (0.000s in global opts, 0.002s io_toposort) - 89 nodes - ('local_dimshuffle_lift', 2) ('local_fill_to_alloc', 1) ('MergeOptimizer', 1) ('local_fill_sink', 1)
       11 - 0.030s 5 (0.000s in global opts, 0.002s io_toposort) - 88 nodes - ('local_dimshuffle_lift', 2) ('local_fill_to_alloc', 1) ('MergeOptimizer', 1) ('constant_folding', 1)
       12 - 0.026s 1 (0.000s in global opts, 0.003s io_toposort) - 81 nodes - ('MergeOptimizer', 1)
       13 - 0.031s 0 (0.000s in global opts, 0.003s io_toposort) - 81 nodes -
       times - times applied - nb node created - name:
       0.263s - 15 - 0 - constant_folding
       0.096s - 2 - 14 - local_greedy_distributor
       0.066s - 4 - 19 - local_mul_canonizer
       0.046s - 28 - 57 - local_fill_sink
       0.042s - 35 - 78 - local_dimshuffle_lift
       0.018s - 5 - 15 - local_upcast_elemwise_constant_inputs
       0.010s - 11 - 4 - MergeOptimizer
       0.009s - 4 - 0 - local_useless_elemwise
       0.005s - 11 - 2 - local_fill_to_alloc
       0.004s - 3 - 6 - local_neg_to_mul
       0.002s - 1 - 3 - local_lift_transpose_through_dot
       0.002s - 3 - 4 - local_shape_to_shape_i
       0.002s - 2 - 4 - local_subtensor_lift
       0.001s - 3 - 0 - local_subtensor_make_vector
       0.001s - 1 - 1 - local_sum_all_to_none
       0.131s - in 62 optimization that where not used (display only those with a runtime > 0)
         0.050s - local_add_canonizer
         0.018s - local_mul_zero
         0.016s - local_one_minus_erf
         0.010s - local_func_inv
         0.006s - local_0_dot_x
         0.005s - local_track_shape_i
         0.004s - local_mul_switch_sink
         0.004s - local_fill_cut
         0.004s - local_one_minus_erf2
         0.003s - local_remove_switch_const_cond
         0.003s - local_cast_cast
         0.002s - local_IncSubtensor_serialize
         0.001s - local_sum_div_dimshuffle
         0.001s - local_div_switch_sink
         0.001s - local_dimshuffle_no_inplace_at_canonicalize
         0.001s - local_cut_useless_reduce
         0.001s - local_reduce_join
         0.000s - local_sum_sum
         0.000s - local_useless_alloc
         0.000s - local_reshape_chain
         0.000s - local_useless_subtensor
         0.000s - local_reshape_lift
         0.000s - local_flatten_lift
         0.000s - local_useless_slice
         0.000s - local_subtensor_of_alloc
         0.000s - local_subtensor_of_dot
         0.000s - local_subtensor_merge
   0.101733s - ('elemwise_fusion', 'SeqOptimizer', 13) - 0.000s
     SeqOptimizer      elemwise_fusion  time 0.102s for 78/50 nodes before/after optimization
       0.000s for fgraph.validate()
       0.004s for callback
       0.095307s - ('composite_elemwise_fusion', 'FusionOptimizer', 1) - 0.000s
         FusionOptimizer
          nb_iter 3
          nb_replacement 10
          nb_inconsistency_replace 0
          validate_time 0.000249624252319
          callback_time 0.00316381454468
          time_toposort 0.00375390052795
       0.006412s - ('local_add_mul_fusion', 'FusionOptimizer', 0) - 0.000s
         FusionOptimizer
          nb_iter 2
          nb_replacement 3
          nb_inconsistency_replace 0
          validate_time 6.43730163574e-05
          callback_time 0.000783205032349
          time_toposort 0.0035240650177
   0.090089s - ('inplace_elemwise_optimizer', 'FromFunctionOptimizer', 30) - 0.019s
   0.048993s - ('BlasOpt', 'SeqOptimizer', 8) - 0.000s
     SeqOptimizer      BlasOpt  time 0.049s for 81/80 nodes before/after optimization
       0.000s for fgraph.validate()
       0.003s for callback
       0.035997s - ('gemm_optimizer', 'GemmOptimizer', 1) - 0.000s
         GemmOptimizer
          nb_iter 2
          nb_replacement 2
          nb_replacement_didn_t_remove 0
          nb_inconsistency_make 0
          nb_inconsistency_replace 0
          time_canonicalize 0.00720071792603
          time_factor_can 9.05990600586e-06
          time_factor_list 0.00128507614136
          time_toposort 0.00311398506165
          validate_time 4.60147857666e-05
          callback_time 0.00174236297607
       0.004569s - ('local_dot_to_dot22', 'TopoOptimizer', 0) - 0.000s
         TopoOptimizer
           nb_node (start, end, changed) (81, 81, 5)
           init io_toposort 0.00139284133911
           loop time 0.00312399864197
           callback_time 0.00172805786133
       0.002283s - ('local_dot22_to_dot22scalar', 'TopoOptimizer', 2) - 0.000s
         TopoOptimizer
           nb_node (start, end, changed) (80, 80, 0)
           init io_toposort 0.00171804428101
           loop time 0.000502109527588
           callback_time 0.0
       0.002257s - ('local_gemm_to_gemv', 'EquilibriumOptimizer', 3) - 0.000s
         EquilibriumOptimizer          local_gemm_to_gemv
           time 0.002s for 1 passes
           nb nodes (start, end,  max) 80 80 80
           time io_toposort 0.001s
           time in local optimizers 0.000s
           time in global optimizers 0.000s
            0 - 0.002s 0 (0.000s in global opts, 0.001s io_toposort) - 80 nodes -
       0.002227s - ('use_c_blas', 'TopoOptimizer', 4) - 0.000s
         TopoOptimizer
           nb_node (start, end, changed) (80, 80, 0)
           init io_toposort 0.0014750957489
           loop time 0.00068998336792
           callback_time 0.0
       0.001632s - ('use_scipy_ger', 'TopoOptimizer', 5) - 0.000s
         TopoOptimizer
           nb_node (start, end, changed) (80, 80, 0)
           init io_toposort 0.00138401985168
           loop time 0.000202178955078
           callback_time 0.0
   0.031740s - ('specialize', 'EquilibriumOptimizer', 9) - 0.000s
     EquilibriumOptimizer      specialize
       time 0.031s for 2 passes
       nb nodes (start, end,  max) 80 78 80
       time io_toposort 0.003s
       time in local optimizers 0.022s
       time in global optimizers 0.004s
        0 - 0.017s 6 (0.002s in global opts, 0.001s io_toposort) - 80 nodes - ('constant_folding', 2) ('local_mul_to_sqr', 1) ('local_elemwise_alloc', 1) ('local_div_to_inv', 1) ('local_mul_specialize', 1)
        1 - 0.014s 0 (0.002s in global opts, 0.001s io_toposort) - 78 nodes -
       times - times applied - nb node created - name:
       0.003s - 1 - 1 - local_mul_specialize
       0.002s - 1 - 2 - local_elemwise_alloc
       0.002s - 2 - 0 - constant_folding
       0.001s - 1 - 1 - local_div_to_inv
       0.001s - 1 - 1 - local_mul_to_sqr
       0.016s - in 69 optimization that where not used (display only those with a runtime > 0)
         0.004s - crossentropy_to_crossentropy_with_softmax_with_bias
         0.002s - local_one_minus_erf
         0.002s - Elemwise{sub,no_inplace}(z, Elemwise{mul,no_inplace}(alpha subject to <function <lambda> at 0x7f475e4da050>, SparseDot(x, y))) -> Usmm{no_inplace}(Elemwise{neg,no_inplace}(alpha), x, y, z)
         0.002s - local_add_specialize
         0.001s - local_func_inv
         0.001s - local_useless_elemwise
         0.001s - local_abs_merge
         0.001s - local_track_shape_i
         0.000s - local_one_minus_erf2
         0.000s - local_sum_mul_by_scalar
         0.000s - local_elemwise_sub_zeros
         0.000s - local_cast_cast
         0.000s - local_alloc_unary
         0.000s - Elemwise{log,no_inplace}(Softmax(x)) -> <function make_out_pattern at 0x7f47619a8410>(x)
         0.000s - local_sum_div_dimshuffle
         0.000s - local_sum_alloc
         0.000s - local_dimshuffle_lift
         0.000s - local_reduce_broadcastable
         0.000s - local_grad_log_erfc_neg
         0.000s - local_advanced_indexing_crossentropy_onehot
         0.000s - local_log_erfc
         0.000s - local_log1p
         0.000s - local_log_add
         0.000s - local_useless_alloc
         0.000s - local_neg_neg
         0.000s - local_neg_div_neg
...

To understand this profile here is some explanation of how optimizations work:

Optimizations are organized in an hierarchy. At the top level, there is a SeqOptimizer (Sequence Optimizer). It contains other optimizers, and applies them in the order they were specified. Those sub-optimizers can be of other types, but are all global optimizers.
Each Optimizer in the hierarchy will print some stats about itself. The information that it prints depends of the type of the optimizer.
The SeqOptimizer will print some stats at the start:
Optimizer Profile ----------------- SeqOptimizer OPT_FAST_RUN time 1.152s for 123/50 nodes before/after optimization 0.028s for fgraph.validate() 0.131s for callback time - (name, class, index) - validate time Then it will print, with some additional indentation, each sub-optimizer's profile information. These sub-profiles are ordered by the time they took to execute, not by their execution order.
- OPT_FAST_RUN is the name of the optimizer
- 1.152s is the total time spent in that optimizer
- 123/50 means that before this optimization, there were 123 apply node in the function graph, and after only 50.
- 0.028s means it spent that time calls to fgraph.validate()
- 0.131s means it spent that time for callbacks. This is a mechanism that can trigger other execution when there is a change to the FunctionGraph.
- time - (name, class, index) - validate time tells how the information for each sub-optimizer get printed.
- All other instances of SeqOptimizer are described like this. In particular, some sub-optimizer from OPT_FAST_RUN that are also SeqOptimizer.

The SeqOptimizer will print some stats at the start:

751816s - ('canonicalize', 'EquilibriumOptimizer', 4) - 0.004s
  EquilibriumOptimizer      canonicalize
    time 0.751s for 14 passes
    nb nodes (start, end,  max) 108 81 117
    time io_toposort 0.029s
    time in local optimizers 0.687s
    time in global optimizers 0.010s
- 0.050s 27 (0.000s in global opts, 0.002s io_toposort) - 108 nodes - ('local_dimshuffle_lift', 9) ('local_upcast_elemwise_constant_inputs', 5) ('local_shape_to_shape_i', 3) ('local_fill_sink', 3) ('local_fill_to_alloc', 2) ...
- 0.288s 26 (0.002s in global opts, 0.002s io_toposort) - 117 nodes - ('local_dimshuffle_lift', 8) ('local_fill_sink', 4) ('constant_folding', 4) ('local_useless_elemwise', 3) ('local_subtensor_make_vector', 3) ...
- 0.044s 13 (0.002s in global opts, 0.003s io_toposort) - 96 nodes - ('constant_folding', 4) ('local_dimshuffle_lift', 3) ('local_fill_sink', 3) ('local_useless_elemwise', 1) ('local_fill_to_alloc', 1) ...
- 0.045s 11 (0.000s in global opts, 0.002s io_toposort) - 91 nodes - ('constant_folding', 3) ('local_fill_to_alloc', 2) ('local_dimshuffle_lift', 2) ('local_mul_canonizer', 2) ('MergeOptimizer', 1) ...
- 0.035s 8 (0.002s in global opts, 0.002s io_toposort) - 93 nodes - ('local_fill_sink', 3) ('local_dimshuffle_lift', 2) ('local_fill_to_alloc', 1) ('MergeOptimizer', 1) ('constant_folding', 1)
- 0.035s 6 (0.000s in global opts, 0.002s io_toposort) - 88 nodes - ('local_fill_sink', 2) ('local_dimshuffle_lift', 2) ('local_fill_to_alloc', 1) ('local_mul_canonizer', 1)
- 0.038s 10 (0.001s in global opts, 0.002s io_toposort) - 95 nodes - ('local_fill_sink', 3) ('local_dimshuffle_lift', 3) ('constant_folding', 2) ('local_fill_to_alloc', 1) ('MergeOptimizer', 1)
- 0.032s 5 (0.001s in global opts, 0.002s io_toposort) - 91 nodes - ('local_fill_sink', 3) ('MergeOptimizer', 1) ('local_dimshuffle_lift', 1)
- 0.034s 5 (0.000s in global opts, 0.002s io_toposort) - 92 nodes - ('local_fill_sink', 3) ('MergeOptimizer', 1) ('local_greedy_distributor', 1)
- 0.031s 6 (0.001s in global opts, 0.002s io_toposort) - 90 nodes - ('local_fill_sink', 2) ('local_fill_to_alloc', 1) ('MergeOptimizer', 1) ('local_dimshuffle_lift', 1) ('local_greedy_distributor', 1)
- 0.032s 5 (0.000s in global opts, 0.002s io_toposort) - 89 nodes - ('local_dimshuffle_lift', 2) ('local_fill_to_alloc', 1) ('MergeOptimizer', 1) ('local_fill_sink', 1)
- 0.030s 5 (0.000s in global opts, 0.002s io_toposort) - 88 nodes - ('local_dimshuffle_lift', 2) ('local_fill_to_alloc', 1) ('MergeOptimizer', 1) ('constant_folding', 1)
- 0.026s 1 (0.000s in global opts, 0.003s io_toposort) - 81 nodes - ('MergeOptimizer', 1)
- 0.031s 0 (0.000s in global opts, 0.003s io_toposort) - 81 nodes -
    times - times applied - nb node created - name:
263s - 15 - 0 - constant_folding
096s - 2 - 14 - local_greedy_distributor
066s - 4 - 19 - local_mul_canonizer
046s - 28 - 57 - local_fill_sink
042s - 35 - 78 - local_dimshuffle_lift
018s - 5 - 15 - local_upcast_elemwise_constant_inputs
010s - 11 - 4 - MergeOptimizer
009s - 4 - 0 - local_useless_elemwise
005s - 11 - 2 - local_fill_to_alloc
004s - 3 - 6 - local_neg_to_mul
002s - 1 - 3 - local_lift_transpose_through_dot
002s - 3 - 4 - local_shape_to_shape_i
002s - 2 - 4 - local_subtensor_lift
001s - 3 - 0 - local_subtensor_make_vector
001s - 1 - 1 - local_sum_all_to_none
131s - in 62 optimization that where not used (display only those with a runtime > 0)
050s - local_add_canonizer
018s - local_mul_zero
016s - local_one_minus_erf
010s - local_func_inv
006s - local_0_dot_x
005s - local_track_shape_i
004s - local_mul_switch_sink
004s - local_fill_cut
004s - local_one_minus_erf2
003s - local_remove_switch_const_cond
003s - local_cast_cast
002s - local_IncSubtensor_serialize
001s - local_sum_div_dimshuffle
001s - local_div_switch_sink
001s - local_dimshuffle_no_inplace_at_canonicalize
001s - local_cut_useless_reduce
001s - local_reduce_join
000s - local_sum_sum
000s - local_useless_alloc
000s - local_reshape_chain
000s - local_useless_subtensor
000s - local_reshape_lift
000s - local_flatten_lift
000s - local_useless_slice
000s - local_subtensor_of_alloc
000s - local_subtensor_of_dot
000s - local_subtensor_merge

0.751816s - ('canonicalize', 'EquilibriumOptimizer', 4) - 0.004s This line is from SeqOptimizer, and indicates information related to a sub-optimizer. It means that this sub-optimizer took a total of .7s. Its name is 'canonicalize'. It is an EquilibriumOptimizer. It was executed at index 4 by the SeqOptimizer. It spent 0.004s in the validate phase.
All other lines are from the profiler of the EquilibriumOptimizer.
An EquilibriumOptimizer does multiple passes on the Apply nodes from the graph, trying to apply local and global optimizations. Conceptually, it tries to execute all global optimizations, and to apply all local optimizations on all nodes in the graph. If no optimization got applied during a pass, it stops. So it tries to find an equilibrium state where none of the optimizations get applied. This is useful when we do not know a fixed order for the execution of the optimization.
time 0.751s for 14 passes means that it took .7s and did 14 passes over the graph.
nb nodes (start, end, max) 108 81 117 means that at the start, the graph had 108 node, at the end, it had 81 and the maximum size was 117.
Then it prints some global timing information: it spent 0.029s in io_toposort, all local optimizers took 0.687s together for all passes, and global optimizers took a total of 0.010s.
Then we print the timing for each pass, the optimization that got applied, and the number of time they got applied. For example, in pass 0, the local_dimshuffle_lift optimizer changed the graph 9 time.
Then we print the time spent in each optimizer, the number of times they changed the graph and the number of nodes they introduced in the graph.
Optimizations with that pattern local_op_lift means that a node with that op will be replaced by another node, with the same op, but will do computation closer to the inputs of the graph. For instance, local_op(f(x)) getting replaced by f(local_op(x)).
Optimization with that pattern local_op_sink is the opposite of lift. For instance f(local_op(x)) getting replaced by local_op(f(x)).
Local optimizers can replace any arbitrary node in the graph, not only the node it received as input. For this, it must return a dict. The keys being nodes to replace and the values being the corresponding replacement.

This is useful to replace a client of the node received as parameter.

Table Of Contents

Previous topic

Next topic

This Page

Graph optimization¶

Global and local optimizations¶

Global optimization¶

Local optimization¶

One simplification rule¶

Global optimization¶

Local optimization¶

OpSub, OpRemove, PatternSub¶

The optimization database (optdb)¶

Definition of optdb¶

Query¶

Examples¶

Registering an Optimizer¶

Registering a LocalOptimizer¶

optdb structure¶

Navigator¶

Profiling Theano function compilation¶

Detailed profiling of Theano optimizer¶