sandbox.linalg – Linear Algebra Ops

API

class theano.sandbox.linalg.ops.Hint(**kwargs)

Provide arbitrary information to the optimizer.

These ops are removed from the graph during canonicalization in order to not interfere with other optimizations. The idea is that prior to canonicalization, one or more Features of the fgraph should register the information contained in any Hint node, and transfer that information out of the graph.

class theano.sandbox.linalg.ops.HintsFeature

FunctionGraph Feature to track matrix properties.

This is a similar feature to variable ‘tags’. In fact, tags are one way to provide hints.

This class exists because tags were not documented well, and the semantics of how tag information should be moved around during optimizations was never clearly spelled out.

Hints are assumptions about mathematical properties of variables. If one variable is substituted for another by an optimization, then it means that the assumptions should be transferred to the new variable.

Hints are attached to ‘positions in a graph’ rather than to variables in particular, although Hints are originally attached to a particular positition in a graph via a variable in that original graph.

Examples of hints are: - shape information - matrix properties (e.g. symmetry, psd, banded, diagonal)

Hint information is propagated through the graph similarly to graph optimizations, except that adding a hint does not change the graph. Adding a hint is not something that debugmode will check.

#TODO: should a Hint be an object that can actually evaluate its # truthfulness? # Should the PSD property be an object that can check the # PSD-ness of a variable?

class theano.sandbox.linalg.ops.HintsOptimizer

Optimizer that serves to add HintsFeature as an fgraph feature.

theano.sandbox.linalg.ops.psd(v)

Apply a hint that the variable v is positive semi-definite, i.e. it is a symmetric matrix and 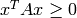x^T A x \ge 0 for any vector x.

theano.sandbox.linalg.ops.spectral_radius_bound(X, log2_exponent)

Returns upper bound on the largest eigenvalue of square symmetrix matrix X.

log2_exponent must be a positive-valued integer. The larger it is, the slower and tighter the bound. Values up to 5 should usually suffice. The algorithm works by multiplying X by itself this many times.

From V.Pan, 1990. “Estimating the Extremal Eigenvalues of a Symmetric Matrix”, Computers Math Applic. Vol 20 n. 2 pp 17-22. Rq: an efficient algorithm, not used here, is defined in this paper.