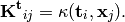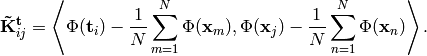Kernels¶
Kernel Functions¶
A kernel is a function  that for all
that for all
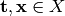 satisfies
satisfies 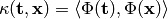 ,
where
,
where 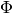 is a mapping from
is a mapping from 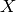 to an (inner product)
feature space
to an (inner product)
feature space 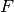 ,
, 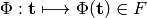 .
.
The following functions take two array-like objects t (M, P) and
x (N, P) and compute the (M, N) matrix  with entries
with entries
Kernel Classes¶
- class mlpy.Kernel¶
Base class for kernels.
- class mlpy.KernelLinear¶
Linear kernel, t_i’ x_j.
- class mlpy.KernelPolynomial(gamma=1.0, b=1.0, d=2.0)¶
Polynomial kernel, (gamma t_i’ x_j + b)^d.
- class mlpy.KernelGaussian(sigma=1.0)¶
Gaussian kernel, exp(-||t_i - x_j||^2 / 2 * sigma^2).
- class mlpy.KernelExponential(sigma=1.0)¶
Exponential kernel, exp(-||t_i - x_j|| / 2 * sigma^2).
- class mlpy.KernelSigmoid(gamma=1.0, b=1.0)¶
Sigmoid kernel, tanh(gamma t_i’ x_j + b).
Functions¶
- mlpy.kernel_linear(t, x)¶
Linear kernel, t_i’ x_j.
- mlpy.kernel_polynomial(t, x, gamma=1.0, b=1.0, d=2.0)¶
Polynomial kernel, (gamma t_i’ x_j + b)^d.
- mlpy.kernel_gaussian(t, x, sigma=1.0)¶
Gaussian kernel, exp(-||t_i - x_j||^2 / 2 * sigma^2).
- mlpy.kernel_exponential(t, x, sigma=1.0)¶
Exponential kernel, exp(-||t_i - x_j|| / 2 * sigma^2).
- mlpy.kernel_sigmoid(t, x, gamma=1.0, b=1.0)¶
Sigmoid kernel, tanh(gamma t_i’ x_j + b).
Example:
>>> import mlpy
>>> x = [[5, 1, 3, 1], [7, 1, 11, 4], [0, 4, 2, 9]] # three training points
>>> K = mlpy.kernel_gaussian(x, x, sigma=10) # compute the kernel matrix K_ij = k(x_i, x_j)
>>> K
array([[ 1. , 0.68045064, 0.60957091],
[ 0.68045064, 1. , 0.44043165],
[ 0.60957091, 0.44043165, 1. ]])
>>> t = [[8, 1, 5, 1], [7, 1, 11, 4]] # two test points
>>> Kt = mlpy.kernel_gaussian(t, x, sigma=10) # compute the test kernel matrix Kt_ij = <Phi(t_i), Phi(x_j)> = k(t_i, x_j)
>>> Kt
array([[ 0.93706746, 0.7945336 , 0.48190899],
[ 0.68045064, 1. , 0.44043165]])
Centering in Feature Space¶
The centered kernel matrix 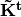 is computed
by:
is computed
by:
We can express 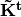 in terms of
in terms of  and
and  :
:
where 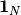 is the
is the 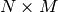 matrix with all
entries equal to
matrix with all
entries equal to 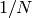 and
and  is
is 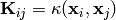 .
.
- mlpy.kernel_center(Kt, K)¶
Centers the testing kernel matrix Kt respect the training kernel matrix K. If Kt = K (kernel_center(K, K), where K = k(x_i, x_j)), the function centers the kernel matrix K.
Parameters : - Kt : 2d array_like object (M, N)
test kernel matrix Kt_ij = k(t_i, x_j). If Kt = K the function centers the kernel matrix K
- K : 2d array_like object (N, N)
training kernel matrix K_ij = k(x_i, x_j)
Returns : - Ktcentered : 2d numpy array (M, N)
centered version of Kt
Example:
>>> Kcentered = mlpy.kernel_center(K, K) # center K
>>> Kcentered
array([[ 0.19119746, -0.07197215, -0.11922531],
[-0.07197215, 0.30395696, -0.23198481],
[-0.11922531, -0.23198481, 0.35121011]])
>>> Ktcentered = mlpy.kernel_center(Kt, K) # center the test kernel matrix Kt respect to K
>>> Ktcentered
array([[ 0.15376875, 0.06761464, -0.22138339],
[-0.07197215, 0.30395696, -0.23198481]])
Make a Custom Kernel¶
TODO
| [Scolkopf98] | Bernhard Scholkopf, Alexander Smola, and Klaus-Robert Muller. Nonlinear component analysis as a kernel eigenvalue problem. Neural Computation, 10(5):1299–1319, July 1998. |