librosa.filters.semitone_filterbank

librosa.filters.semitone_filterbank(center_freqs=None, tuning=0.0, sample_rates=None, **kwargs)

Constructs a filterbank with 88 filters mimicing the equal-tempered scale.

When run with default parameters, a filter bank with 88 filters, each having a bandwith of one semitone, is designed. For details, see [1].

[1]	Müller, Meinard. “Information Retrieval for Music and Motion.” Springer Verlag. 2007.

Parameters:

center_freqs : np.ndarray [shape=(n,), dtype=float]

Center frequencies of the filter kernels. Also defines the number of filters in the filterbank.

tuning : float in [-0.5, +0.5) [scalar]

Tuning deviation from A440 in fractions of a bin.

sample_rates : np.ndarray [shape=(n,), dtype=float]

Samplerate for each filter (used for multirate filterbank).

kwargs : additional keyword arguments

Additional arguments for multirate_fb().

Returns:

filterbank : list [shape=(n,), dtype=float]

Each list entry comprises the filter coefficients for a single filter.

fb_sample_rates : np.ndarray [shape=(n,), dtype=float]

Samplerate for each filter.

See also

librosa.filters.multirate_fb, librosa.core.semitone_spectrogram, librosa.core.cqt, scipy.signal.iirdesign

Examples

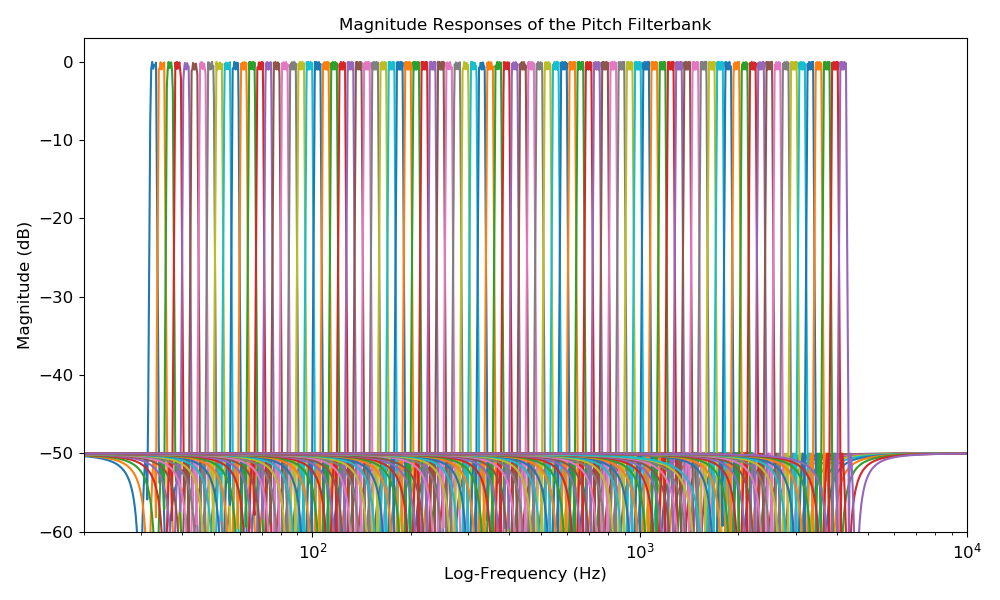
>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> import scipy.signal
>>> semitone_filterbank, sample_rates = librosa.filters.semitone_filterbank()
>>> plt.figure(figsize=(10, 6))
>>> for cur_sr, cur_filter in zip(sample_rates, semitone_filterbank):
...    w, h = scipy.signal.freqz(cur_filter[0], cur_filter[1], worN=2000)
...    plt.plot((cur_sr / (2 * np.pi)) * w, 20 * np.log10(abs(h)))
>>> plt.semilogx()
>>> plt.xlim([20, 10e3])
>>> plt.ylim([-60, 3])
>>> plt.title('Magnitude Responses of the Pitch Filterbank')
>>> plt.xlabel('Log-Frequency (Hz)')
>>> plt.ylabel('Magnitude (dB)')
>>> plt.tight_layout()

(Source code)