Basic Tensor Functionality¶

Theano supports any kind of Python object, but its focus is support for symbolic matrix expressions. When you type,

>>> x = T.fmatrix()

the x is a TensorVariable instance. The T.fmatrix object itself is an instance of TensorType. Theano knows what type of variable x is because x.type points back to T.fmatrix.

This chapter explains the various ways of creating tensor variables, the attributes and methods of TensorVariable and TensorType, and various basic symbolic math and arithmetic that Theano supports for tensor variables.

Creation¶

Theano provides a list of predefined tensor types that can be used to create a tensor variables. Variables can be named to facilitate debugging, and all of these constructors accept an optional name argument. For example, the following each produce a TensorVariable instance that stands for a 0-dimensional ndarray of integers with the name 'myvar':

>>> x = scalar('myvar', dtype='int32')
>>> x = iscalar('myvar')
>>> x = TensorType(dtype='int32', broadcastable=())('myvar')

Constructors with optional dtype¶

These are the simplest and often-preferred methods for creating symbolic variables in your code. By default, they produce floating-point variables (with dtype determined by config.floatX, see floatX) so if you use these constructors it is easy to switch your code between different levels of floating-point precision.

theano.tensor.scalar(name=None, dtype=config.floatX)¶: Return a Variable for a 0-dimensional ndarray

theano.tensor.vector(name=None, dtype=config.floatX)¶: Return a Variable for a 1-dimensional ndarray

theano.tensor.row(name=None, dtype=config.floatX)¶: Return a Variable for a 2-dimensional ndarray in which the number of rows is guaranteed to be 1.

theano.tensor.col(name=None, dtype=config.floatX)¶: Return a Variable for a 2-dimensional ndarray in which the number of columns is guaranteed to be 1.

theano.tensor.matrix(name=None, dtype=config.floatX)¶: Return a Variable for a 2-dimensional ndarray

theano.tensor.tensor3(name=None, dtype=config.floatX)¶: Return a Variable for a 3-dimensional ndarray

theano.tensor.tensor4(name=None, dtype=config.floatX)¶: Return a Variable for a 4-dimensional ndarray

All Fully-Typed Constructors¶

The following TensorType instances are provided in the theano.tensor module. They are all callable, and accept an optional name argument. So for example:

from theano.tensor import *

x = dmatrix()        # creates one Variable with no name
x = dmatrix('x')     # creates one Variable with name 'x'
xyz = dmatrix('xyz') # creates one Variable with name 'xyz'

Constructor	dtype	ndim	shape	broadcastable
bscalar	int8	0	()	()
bvector	int8	1	(?,)	(False,)
brow	int8	2	(1,?)	(True, False)
bcol	int8	2	(?,1)	(False, True)
bmatrix	int8	2	(?,?)	(False, False)
btensor3	int8	3	(?,?,?)	(False, False, False)
btensor4	int8	4	(?,?,?,?)	(False, False, False, False)
wscalar	int16	0	()	()
wvector	int16	1	(?,)	(False,)
wrow	int16	2	(1,?)	(True, False)
wcol	int16	2	(?,1)	(False, True)
wmatrix	int16	2	(?,?)	(False, False)
wtensor3	int16	3	(?,?,?)	(False, False, False)
wtensor4	int16	4	(?,?,?,?)	(False, False, False, False)
iscalar	int32	0	()	()
ivector	int32	1	(?,)	(False,)
irow	int32	2	(1,?)	(True, False)
icol	int32	2	(?,1)	(False, True)
imatrix	int32	2	(?,?)	(False, False)
itensor3	int32	3	(?,?,?)	(False, False, False)
itensor4	int32	4	(?,?,?,?)	(False, False, False, False)
lscalar	int64	0	()	()
lvector	int64	1	(?,)	(False,)
lrow	int64	2	(1,?)	(True, False)
lcol	int64	2	(?,1)	(False, True)
lmatrix	int64	2	(?,?)	(False, False)
ltensor3	int64	3	(?,?,?)	(False, False, False)
ltensor4	int64	4	(?,?,?,?)	(False, False, False, False)
dscalar	float64	0	()	()
dvector	float64	1	(?,)	(False,)
drow	float64	2	(1,?)	(True, False)
dcol	float64	2	(?,1)	(False, True)
dmatrix	float64	2	(?,?)	(False, False)
dtensor3	float64	3	(?,?,?)	(False, False, False)
dtensor4	float64	4	(?,?,?,?)	(False, False, False, False)
fscalar	float32	0	()	()
fvector	float32	1	(?,)	(False,)
frow	float32	2	(1,?)	(True, False)
fcol	float32	2	(?,1)	(False, True)
fmatrix	float32	2	(?,?)	(False, False)
ftensor3	float32	3	(?,?,?)	(False, False, False)
ftensor4	float32	4	(?,?,?,?)	(False, False, False, False)
cscalar	complex64	0	()	()
cvector	complex64	1	(?,)	(False,)
crow	complex64	2	(1,?)	(True, False)
ccol	complex64	2	(?,1)	(False, True)
cmatrix	complex64	2	(?,?)	(False, False)
ctensor3	complex64	3	(?,?,?)	(False, False, False)
ctensor4	complex64	4	(?,?,?,?)	(False, False, False, False)
zscalar	complex128	0	()	()
zvector	complex128	1	(?,)	(False,)
zrow	complex128	2	(1,?)	(True, False)
zcol	complex128	2	(?,1)	(False, True)
zmatrix	complex128	2	(?,?)	(False, False)
ztensor3	complex128	3	(?,?,?)	(False, False, False)
ztensor4	complex128	4	(?,?,?,?)	(False, False, False, False)

Plural Constructors¶

There are several constructors that can produce multiple variables at once. These are not frequently used in practice, but often used in tutorial examples to save space!

iscalars, lscalars, fscalars, dscalars: Return one or more scalar variables.

ivectors, lvectors, fvectors, dvectors: Return one or more vector variables.

irows, lrows, frows, drows: Return one or more row variables.

icols, lcols, fcols, dcols: Return one or more col variables.

imatrices, lmatrices, fmatrices, dmatrices: Return one or more matrix variables.

Each of these plural constructors accepts an integer or several strings. If an integer is provided, the method will return that many Variables and if strings are provided, it will create one Variable for each string, using the string as the Variable’s name. For example:

from theano.tensor import *

x, y, z = dmatrices(3) # creates three matrix Variables with no names
x, y, z = dmatrices('x', 'y', 'z') # creates three matrix Variables named 'x', 'y' and 'z'

Custom tensor types¶

If you would like to construct a tensor variable with a non-standard broadcasting pattern, or a larger number of dimensions you’ll need to create your own TensorType instance. You create such an instance by passing the dtype and broadcasting pattern to the constructor. For example, you can create your own 5-dimensional tensor type

>>> dtensor5 = TensorType('float64', (False,)*5)
>>> x = dtensor5()
>>> z = dtensor5('z')

You can also redefine some of the provided types and they will interact correctly:

>>> my_dmatrix = TensorType('float64', (False,)*2)
>>> x = my_dmatrix()       # allocate a matrix variable
>>> my_dmatrix == dmatrix
True

See TensorType for more information about creating new types of Tensor.

Converting from Python Objects¶

Another way of creating a TensorVariable (a TensorSharedVariable to be precise) is by calling shared()

x = shared(numpy.random.randn(3,4))

This will return a shared variable whose .value is a numpy ndarray. The number of dimensions and dtype of the Variable are inferred from the ndarray argument. The argument to shared will not be copied, and subsequent changes will be reflected in x.value.

For additional information, see the shared() documentation.

Finally, when you use a numpy ndarry or a Python number together with TensorVariable instances in arithmetic expressions, the result is a TensorVariable. What happens to the ndarray or the number? Theano requires that the inputs to all expressions be Variable instances, so Theano automatically wraps them in a TensorConstant.

Note

Theano makes a copy of any ndarray that you use in an expression, so subsequent changes to that ndarray will not have any effect on the Theano expression.

For numpy ndarrays the dtype is given, but the broadcastable pattern must be inferred. The TensorConstant is given a type with a matching dtype, and a broadcastable pattern with a True for every shape dimension that is 1.

For python numbers, the broadcastable pattern is () but the dtype must be inferred. Python integers are stored in the smallest dtype that can hold them, so small constants like 1 are stored in a bscalar. Likewise, Python floats are stored in an fscalar if fscalar suffices to hold them perfectly, but a dscalar otherwise.

Note

When config.floatX==float32 (see config), then Python floats are stored instead as single-precision floats.

For fine control of this rounding policy, see theano.tensor.basic.autocast_float.

theano.tensor.as_tensor_variable(x, name=None, ndim=None)¶

Turn an argument x into a TensorVariable or TensorConstant.

Many tensor Ops run their arguments through this function as pre-processing. It passes through TensorVariable instances, and tries to wrap other objects into TensorConstant.

When x is a Python number, the dtype is inferred as described above.

When x is a list or tuple it is passed through numpy.asarray

If the ndim argument is not None, it must be an integer and the output will be broadcasted if necessary in order to have this many dimensions.

Return type:	`TensorVariable` or `TensorConstant`

TensorType and TensorVariable¶

class theano.tensor.TensorType(Type)¶

The Type class used to mark Variables that stand for numpy.ndarray values (numpy.memmap, which is a subclass of numpy.ndarray, is also allowed). Recalling to the tutorial, the purple box in the tutorial’s graph-structure figure is an instance of this class.

broadcastable¶

A tuple of True/False values, one for each dimension. True in position ‘i’ indicates that at evaluation-time, the ndarray will have size 1 in that ‘i’-th dimension. Such a dimension is called a broadcastable dimension (see Broadcasting in Theano vs. Numpy).

The broadcastable pattern indicates both the number of dimensions and whether a particular dimension must have length 1.

Here is a table mapping some broadcastable patterns to what they mean:

pattern	interpretation
[]	scalar
[True]	1D scalar (vector of length 1)
[True, True]	2D scalar (1x1 matrix)
[False]	vector
[False, False]	matrix
[False] * n	nD tensor
[True, False]	row (1xN matrix)
[False, True]	column (Mx1 matrix)
[False, True, False]	A Mx1xP tensor (a)
[True, False, False]	A 1xNxP tensor (b)
[False, False, False]	A MxNxP tensor (pattern of a + b)

For dimensions in which broadcasting is False, the length of this dimension can be 1 or more. For dimensions in which broadcasting is True, the length of this dimension must be 1.

When two arguments to an element-wise operation (like addition or subtraction) have a different number of dimensions, the broadcastable pattern is expanded to the left, by padding with True. For example, a vector’s pattern, [False], could be expanded to [True, False], and would behave like a row (1xN matrix). In the same way, a matrix ([False, False]) would behave like a 1xNxP tensor ([True, False, False]).

If we wanted to create a type representing a matrix that would broadcast over the middle dimension of a 3-dimensional tensor when adding them together, we would define it like this:

>>> middle_broadcaster = TensorType('complex64', [False, True, False])

ndim¶: The number of dimensions that a Variable’s value will have at evaluation-time. This must be known when we are building the expression graph.

dtype¶

A string indicating the numerical type of the ndarray for which a Variable of this Type is standing.

The dtype attribute of a TensorType instance can be any of the following strings.

dtype	domain	bits
`'int8'`	signed integer	8
`'int16'`	signed integer	16
`'int32'`	signed integer	32
`'int64'`	signed integer	64
`'uint8'`	unsigned integer	8
`'uint16'`	unsigned integer	16
`'uint32'`	unsigned integer	32
`'uint64'`	unsigned integer	64
`'float32'`	floating point	32
`'float64'`	floating point	64
`'complex64'`	complex	64 (two float32)
`'complex128'`	complex	128 (two float64)

__init__(self, dtype, broadcastable)¶: If you wish to use a type of tensor which is not already available (for example, a 5D tensor) you can build an appropriate type by instantiating TensorType.

TensorVariable¶

class theano.tensor.TensorVariable(Variable, _tensor_py_operators)¶

The result of symbolic operations typically have this type.

See _tensor_py_operators for most of the attributes and methods you’ll want to call.

class theano.tensor.TensorConstant(Variable, _tensor_py_operators)¶

Python and numpy numbers are wrapped in this type.

See _tensor_py_operators for most of the attributes and methods you’ll want to call.

class theano.tensor.TensorSharedVariable(Variable, _tensor_py_operators)¶

This type is returned by shared() when the value to share is a numpy ndarray.

See _tensor_py_operators for most of the attributes and methods you’ll want to call.

class theano.tensor._tensor_py_operators¶

This mix-in class adds convenient attributes, methods, and support to TensorVariable, TensorConstant and TensorSharedVariable for Python operators (see Operator Support).

type¶

A reference to the TensorType instance describing the sort of values that might be associated with this variable.

ndim¶

The number of dimensions of this tensor. Aliased to TensorType.ndim.

dtype¶

The numeric type of this tensor. Aliased to TensorType.dtype.

reshape(shape, ndim=None)¶

Returns a view of this tensor that has been reshaped as in numpy.reshape. If the shape is a Variable argument, then you might need to use the optional ndim parameter to declare how many elements the shape has, and therefore how many dimensions the reshaped Variable will have.

See reshape().

dimshuffle(*pattern)¶

Returns a view of this tensor with permuted dimensions. Typically the pattern will include the integers 0, 1, ... ndim-1, and any number of ‘x’ characters in dimensions where this tensor should be broadcasted.

A few examples of patterns and their effect:

(‘x’) -> make a 0d (scalar) into a 1d vector

(0, 1) -> identity for 2d vectors

(1, 0) -> inverts the first and second dimensions

(‘x’, 0) -> make a row out of a 1d vector (N to 1xN)

(0, ‘x’) -> make a column out of a 1d vector (N to Nx1)

(2, 0, 1) -> AxBxC to CxAxB

(0, ‘x’, 1) -> AxB to Ax1xB

(1, ‘x’, 0) -> AxB to Bx1xA

(1,) -> This remove dimensions 0. It must be a broadcastable dimension (1xA to A)

flatten(ndim=1)¶

Returns a view of this tensor with ndim dimensions, whose shape for the first ndim-1 dimensions will be the same as self, and shape in the remaining dimension will be expanded to fit in all the data from self.

See flatten().

ravel()¶

return self.flatten(). For NumPy compatibility.
T¶
Transpose of this tensor.
>>> x = T.zmatrix()
>>> y = 3+.2j * x.T
Note

In numpy and in Theano, the transpose of a vector is exactly the same vector! Use reshape or dimshuffle to turn your vector into a row or column matrix.
{any,all}(axis=None, keepdims=False)

{sum,prod,mean}(axis=None, dtype=None, keepdims=False, acc_dtype=None)

{var,std,min,max,argmin,argmax}(axis=None, keepdims=False),

diagonal(offset=0, axis1=0, axis2=1)¶

astype(dtype)¶

take(indices, axis=None, mode='raise')¶

copy() Return a new symbolic variable that is a copy of the variable. Does not copy the tag.

norm(L, axis=None)¶

nonzero(self, return_matrix=False)¶

nonzero_values(self)¶

sort(self, axis=-1, kind='quicksort', order=None)¶

argsort(self, axis=-1, kind='quicksort', order=None)¶

clip(self, a_min, a_max)¶

conf()¶

repeat(repeats, axis=None)¶

round(mode="half_away_from_zero")¶

trace()¶

get_scalar_constant_value()¶

zeros_like(model, dtype=None)¶

All the above methods are equivalent to NumPy for Theano on the current tensor.

__{abs,neg,lt,le,gt,ge,invert,and,or,add,sub,mul,div,truediv,floordiv}__

Those elemwise operation are supported via Python syntax.

argmax(axis=None, keepdims=False)¶: See theano.tensor.argmax.

argmin(axis=None, keepdims=False)¶: See theano.tensor.argmin.

argsort(axis=-1, kind='quicksort', order=None): See theano.tensor.argsort.

broadcastable¶: The broadcastable signature of this tensor.

See also

broadcasting

choose(a, choices, out=None, mode='raise')¶: Construct an array from an index array and a set of arrays to choose from.

clip(a_min, a_max): Clip (limit) the values in an array.

compress(a, axis=None)¶: Return selected slices only.

conj()¶: See theano.tensor.conj.

conjugate()¶: See theano.tensor.conj.

copy(name=None)¶

Return a symbolic copy and optionally assign a name.

Does not copy the tags.

dimshuffle(*pattern)

Reorder the dimensions of this variable, optionally inserting broadcasted dimensions.

Parameters:	pattern – List/tuple of int mixed with ‘x’ for broadcastable dimensions.

Examples

For example, to create a 3D view of a [2D] matrix, call dimshuffle([0,'x',1]). This will create a 3D view such that the middle dimension is an implicit broadcasted dimension. To do the same thing on the transpose of that matrix, call dimshuffle([1, 'x', 0]).

Notes

This function supports the pattern passed as a tuple, or as a variable-length argument (e.g. a.dimshuffle(pattern) is equivalent to a.dimshuffle(*pattern) where pattern is a list/tuple of ints mixed with ‘x’ characters).

Shaping and Shuffling¶

To re-order the dimensions of a variable, to insert or remove broadcastable dimensions, see _tensor_py_operators.dimshuffle().

theano.tensor.shape(x)¶: Returns an lvector representing the shape of x.

theano.tensor.reshape(x, newshape, ndim=None)¶

Parameters:	x (any TensorVariable (or compatible)) – variable to be reshaped newshape (lvector (or compatible)) – the new shape for x ndim – optional - the length that newshape‘s value will have. If this is `None`, then reshape() will infer it from newshape.
Return type:	variable with x’s dtype, but ndim dimensions

Note

This function can infer the length of a symbolic newshape in some cases, but if it cannot and you do not provide the ndim, then this function will raise an Exception.

theano.tensor.shape_padleft(x, n_ones=1)¶

Reshape x by left padding the shape with n_ones 1s. Note that all this new dimension will be broadcastable. To make them non-broadcastable see the unbroadcast().

Parameters:	x (any TensorVariable (or compatible)) – variable to be reshaped

theano.tensor.shape_padright(x, n_ones=1)¶

Reshape x by right padding the shape with n_ones 1s. Note that all this new dimension will be broadcastable. To make them non-broadcastable see the unbroadcast().

Parameters:	x (any TensorVariable (or compatible)) – variable to be reshaped

theano.tensor.shape_padaxis(t, axis)¶

Reshape t by inserting 1 at the dimension axis. Note that this new dimension will be broadcastable. To make it non-broadcastable see the unbroadcast().

Parameters:	x (any TensorVariable (or compatible)) – variable to be reshaped axis (int) – axis where to add the new dimension to x

Example:

>>> tensor = theano.tensor.tensor3()
>>> theano.tensor.shape_padaxis(tensor, axis=0)
DimShuffle{x,0,1,2}.0
>>> theano.tensor.shape_padaxis(tensor, axis=1)
DimShuffle{0,x,1,2}.0
>>> theano.tensor.shape_padaxis(tensor, axis=3)
DimShuffle{0,1,2,x}.0
>>> theano.tensor.shape_padaxis(tensor, axis=-1)
DimShuffle{0,1,2,x}.0

theano.tensor.unbroadcast(x, *axes)¶

Make the input impossible to broadcast in the specified axes.

For example, addbroadcast(x, 0) will make the first dimension of x broadcastable. When performing the function, if the length of x along that dimension is not 1, a ValueError will be raised.

We apply the opt here not to pollute the graph especially during the gpu optimization

Parameters:	x (tensor_like) – Input theano tensor. axis (an int or an iterable object such as list or tuple of int values) – The dimension along which the tensor x should be unbroadcastable. If the length of x along these dimensions is not 1, a ValueError will be raised.
Returns:	A theano tensor, which is unbroadcastable along the specified dimensions.
Return type:	tensor

theano.tensor.addbroadcast(x, *axes)¶

Make the input broadcastable in the specified axes.

For example, addbroadcast(x, 0) will make the first dimension of x broadcastable. When performing the function, if the length of x along that dimension is not 1, a ValueError will be raised.

We apply the opt here not to pollute the graph especially during the gpu optimization

Parameters:	x (tensor_like) – Input theano tensor. axis (an int or an iterable object such as list or tuple of int values) – The dimension along which the tensor x should be broadcastable. If the length of x along these dimensions is not 1, a ValueError will be raised.
Returns:	A theano tensor, which is broadcastable along the specified dimensions.
Return type:	tensor

theano.tensor.patternbroadcast(x, broadcastable)¶

Make the input adopt a specific broadcasting pattern.

Broadcastable must be iterable. For example, patternbroadcast(x, (True, False)) will make the first dimension of x broadcastable and the second dimension not broadcastable, so x will now be a row.

We apply the opt here not to pollute the graph especially during the gpu optimization.

Parameters:	x (tensor_like) – Input theano tensor. broadcastable (an iterable object such as list or tuple of bool values) – A set of boolean values indicating whether a dimension should be broadcastable or not. If the length of x along these dimensions is not 1, a ValueError will be raised.
Returns:	A theano tensor, which is unbroadcastable along the specified dimensions.
Return type:	tensor

theano.tensor.flatten(x, outdim=1)¶

Similar to reshape(), but the shape is inferred from the shape of x.

Parameters:	x (any TensorVariable (or compatible)) – variable to be flattened outdim (int) – the number of dimensions in the returned variable
Return type:	variable with same dtype as x and outdim dimensions
Returns:	variable with the same shape as x in the leading outdim-1 dimensions, but with all remaining dimensions of x collapsed into the last dimension.

For example, if we flatten a tensor of shape (2, 3, 4, 5) with flatten(x, outdim=2), then we’ll have the same (2-1=1) leading dimensions (2,), and the remaining dimensions are collapsed. So the output in this example would have shape (2, 60).

theano.tensor.tile(x, reps, ndim=None)¶

Construct an array by repeating the input x according to reps pattern.

Tiles its input according to reps. The length of reps is the number of dimension of x and contains the number of times to tile x in each dimension.

See:	numpy.tile documentation for examples.
See:	`theano.tensor.extra_ops.repeat`
Note:	Currently, reps must be a constant, x.ndim and len(reps) must be equal and, if specified, ndim must be equal to both.

theano.tensor.roll(x, shift, axis=None)¶

Convenience function to roll TensorTypes along the given axis.

Syntax copies numpy.roll function.

Parameters:	x (tensor_like) – Input tensor. shift (int (symbolic or literal)) – The number of places by which elements are shifted. axis (int (symbolic or literal), optional) – The axis along which elements are shifted. By default, the array is flattened before shifting, after which the original shape is restored.
Returns:	Output tensor, with the same shape as `x`.
Return type:	tensor

Creating Tensor¶

theano.tensor.zeros_like(x)¶

Parameters:	x – tensor that has same shape as output

Returns a tensor filled with 0s that has same shape as x.

theano.tensor.ones_like(x)¶

Parameters:	x – tensor that has same shape as output

Returns a tensor filled with 1s that has same shape as x.

theano.tensor.fill(a, b)¶

Parameters:	a – tensor that has same shape as output b – theano scalar or value with which you want to fill the output

Create a matrix by filling the shape of a with b

theano.tensor.alloc(value, *shape)¶

Parameters:	value – a value with which to fill the output shape – the dimensions of the returned array
Returns:	an N-dimensional tensor initialized by value and having the specified shape.

theano.tensor.eye(n, m=None, k=0, dtype=theano.config.floatX)¶

Parameters:	n – number of rows in output (value or theano scalar) m – number of columns in output (value or theano scalar) k – Index of the diagonal: 0 refers to the main diagonal, a positive value refers to an upper diagonal, and a negative value to a lower diagonal. It can be a theano scalar.
Returns:	An array where all elements are equal to zero, except for the k-th diagonal, whose values are equal to one.

theano.tensor.identity_like(x)¶

Parameters:	x – tensor
Returns:	A tensor of same shape as x that is filled with 0s everywhere except for the main diagonal, whose values are equal to one. The output will have same dtype as x.

theano.tensor.stack(tensors, axis=0)¶

Stack tensors in sequence on given axis (default is 0).

Take a sequence of tensors and stack them on given axis to make a single tensor. The size in dimension axis of the result will be equal to the number of tensors passed.

Parameters:	tensors – a list or a tuple of one or more tensors of the same rank. axis – the axis along which the tensors will be stacked. Default value is 0.
Returns:	A tensor such that rval[0] == tensors[0], rval[1] == tensors[1], etc.

Examples:

>>> a = theano.tensor.scalar()
>>> b = theano.tensor.scalar()
>>> c = theano.tensor.scalar()
>>> x = theano.tensor.stack([a, b, c])
>>> x.ndim # x is a vector of length 3.
1
>>> a = theano.tensor.tensor4()
>>> b = theano.tensor.tensor4()
>>> c = theano.tensor.tensor4()
>>> x = theano.tensor.stack([a, b, c])
>>> x.ndim # x is a 5d tensor.
5
>>> rval = x.eval(dict((t, np.zeros((2, 2, 2, 2))) for t in [a, b, c]))
>>> rval.shape # 3 tensors are stacked on axis 0
(3, 2, 2, 2, 2)

We can also specify different axis than default value 0

>>> x = theano.tensor.stack([a, b, c], axis=3)
>>> x.ndim
5
>>> rval = x.eval(dict((t, np.zeros((2, 2, 2, 2))) for t in [a, b, c]))
>>> rval.shape # 3 tensors are stacked on axis 3
(2, 2, 2, 3, 2)
>>> x = theano.tensor.stack([a, b, c], axis=-2)
>>> x.ndim
5
>>> rval = x.eval(dict((t, np.zeros((2, 2, 2, 2))) for t in [a, b, c]))
>>> rval.shape # 3 tensors are stacked on axis -2
(2, 2, 2, 3, 2)

theano.tensor.stack(*tensors)

Warning

The interface stack(*tensors) is deprecated! Use stack(tensors, axis=0) instead.

Stack tensors in sequence vertically (row wise).

Take a sequence of tensors and stack them vertically to make a single tensor.

Parameters:	tensors – one or more tensors of the same rank
Returns:	A tensor such that rval[0] == tensors[0], rval[1] == tensors[1], etc.

>>> x0 = T.scalar()
>>> x1 = T.scalar()
>>> x2 = T.scalar()
>>> x = T.stack(x0, x1, x2)
>>> x.ndim # x is a vector of length 3.
1

theano.tensor.concatenate(tensor_list, axis=0)¶

Parameters:	tensor_list (a list or tuple of Tensors that all have the same shape in the axes not specified by the axis argument.) – one or more Tensors to be concatenated together into one. axis (literal or symbolic integer) – Tensors will be joined along this axis, so they may have different `shape[axis]`

>>> x0 = T.fmatrix()
>>> x1 = T.ftensor3()
>>> x2 = T.fvector()
>>> x = T.concatenate([x0, x1[0], T.shape_padright(x2)], axis=1)
>>> x.ndim
2

theano.tensor.stacklists(tensor_list)¶

Parameters:	tensor_list (an iterable that contains either tensors or other iterables of the same type as tensor_list (in other words, this is a tree whose leaves are tensors).) – tensors to be stacked together.

Recursively stack lists of tensors to maintain similar structure.

This function can create a tensor from a shaped list of scalars:

>>> from theano.tensor import stacklists, scalars, matrices
>>> from theano import function
>>> a, b, c, d = scalars('abcd')
>>> X = stacklists([[a, b], [c, d]])
>>> f = function([a, b, c, d], X)
>>> f(1, 2, 3, 4)
array([[ 1.,  2.],
       [ 3.,  4.]])

We can also stack arbitrarily shaped tensors. Here we stack matrices into a 2 by 2 grid:

>>> from numpy import ones
>>> a, b, c, d = matrices('abcd')
>>> X = stacklists([[a, b], [c, d]])
>>> f = function([a, b, c, d], X)
>>> x = ones((4, 4), 'float32')
>>> f(x, x, x, x).shape
(2, 2, 4, 4)

theano.tensor.basic.choose(a, choices, out=None, mode='raise')¶

Construct an array from an index array and a set of arrays to choose from.

First of all, if confused or uncertain, definitely look at the Examples - in its full generality, this function is less simple than it might seem from the following code description (below ndi = numpy.lib.index_tricks):

np.choose(a,c) == np.array([c[a[I]][I] for I in ndi.ndindex(a.shape)]).

But this omits some subtleties. Here is a fully general summary:

Given an index array (a) of integers and a sequence of n arrays (choices), a and each choice array are first broadcast, as necessary, to arrays of a common shape; calling these Ba and Bchoices[i], i = 0,...,n-1 we have that, necessarily, Ba.shape == Bchoices[i].shape for each i. Then, a new array with shape Ba.shape is created as follows:

if mode=raise (the default), then, first of all, each element of a (and thus Ba) must be in the range [0, n-1]; now, suppose that i (in that range) is the value at the (j0, j1, ..., jm) position in Ba - then the value at the same position in the new array is the value in Bchoices[i] at that same position;
if mode=wrap, values in a (and thus Ba) may be any (signed) integer; modular arithmetic is used to map integers outside the range [0, n-1] back into that range; and then the new array is constructed as above;
if mode=clip, values in a (and thus Ba) may be any (signed) integer; negative integers are mapped to 0; values greater than n-1 are mapped to n-1; and then the new array is constructed as above.

Parameters:	a (int array) – This array must contain integers in [0, n-1], where n is the number of choices, unless mode=wrap or mode=clip, in which cases any integers are permissible. choices (sequence of arrays) – Choice arrays. a and all of the choices must be broadcastable to the same shape. If choices is itself an array (not recommended), then its outermost dimension (i.e., the one corresponding to choices.shape[0]) is taken as defining the `sequence`. out (array, optional) – If provided, the result will be inserted into this array. It should be of the appropriate shape and dtype. mode ({`raise` (default), `wrap`, `clip`}, optional) – Specifies how indices outside [0, n-1] will be treated: `raise` : an exception is raised `wrap` : value becomes value mod n `clip` : values < 0 are mapped to 0, values > n-1 are mapped to n-1
Returns:	The merged result.
Return type:	merged_array - array
Raises:	ValueError - shape mismatch – If a and each choice array are not all broadcastable to the same shape.

Reductions¶

theano.tensor.max(x, axis=None, keepdims=False)¶

Parameter:	x - symbolic Tensor (or compatible)
Parameter:	axis - axis or axes along which to compute the maximum
Parameter:	keepdims - (boolean) If this is set to True, the axes which are reduced are left in the result as dimensions with size one. With this option, the result will broadcast correctly against the original tensor.
Returns:	maximum of x along axis

axis can be:

None - in which case the maximum is computed along all axes (like numpy)
an int - computed along this axis
a list of ints - computed along these axes

theano.tensor.argmax(x, axis=None, keepdims=False)¶

Parameter:	x - symbolic Tensor (or compatible)
Parameter:	axis - axis along which to compute the index of the maximum
Parameter:	keepdims - (boolean) If this is set to True, the axis which is reduced is left in the result as a dimension with size one. With this option, the result will broadcast correctly against the original tensor.
Returns:	the index of the maximum value along a given axis

if axis=None, Theano 0.5rc1 or later: argmax over the flattened tensor (like numpy): older: then axis is assumed to be ndim(x)-1

theano.tensor.max_and_argmax(x, axis=None, keepdims=False)¶

Parameter:	x - symbolic Tensor (or compatible)
Parameter:	axis - axis along which to compute the maximum and its index
Parameter:	keepdims - (boolean) If this is set to True, the axis which is reduced is left in the result as a dimension with size one. With this option, the result will broadcast correctly against the original tensor.
Returns:	the maxium value along a given axis and its index.

if axis=None, Theano 0.5rc1 or later: max_and_argmax over the flattened tensor (like numpy): older: then axis is assumed to be ndim(x)-1

theano.tensor.min(x, axis=None, keepdims=False)¶

Parameter:	x - symbolic Tensor (or compatible)
Parameter:	axis - axis or axes along which to compute the minimum
Parameter:	keepdims - (boolean) If this is set to True, the axes which are reduced are left in the result as dimensions with size one. With this option, the result will broadcast correctly against the original tensor.
Returns:	minimum of x along axis

axis can be:

None - in which case the minimum is computed along all axes (like numpy)
an int - computed along this axis
a list of ints - computed along these axes

theano.tensor.argmin(x, axis=None, keepdims=False)¶

Parameter:	x - symbolic Tensor (or compatible)
Parameter:	axis - axis along which to compute the index of the minimum
Parameter:	keepdims - (boolean) If this is set to True, the axes which are reduced are left in the result as dimensions with size one. With this option, the result will broadcast correctly against the original tensor.
Returns:	the index of the minimum value along a given axis

if axis=None, Theano 0.5rc1 or later: argmin over the flattened tensor (like numpy): older: then axis is assumed to be ndim(x)-1

theano.tensor.sum(x, axis=None, dtype=None, keepdims=False, acc_dtype=None)¶

Parameter:	x - symbolic Tensor (or compatible)
Parameter:	axis - axis or axes along which to compute the sum
Parameter:	dtype - The dtype of the returned tensor. If None, then we use the default dtype which is the same as the input tensor’s dtype except when: the input dtype is a signed integer of precision < 64 bit, in which case we use int64 the input dtype is an unsigned integer of precision < 64 bit, in which case we use uint64 This default dtype does _not_ depend on the value of “acc_dtype”.
Parameter:	keepdims - (boolean) If this is set to True, the axes which are reduced are left in the result as dimensions with size one. With this option, the result will broadcast correctly against the original tensor.
Parameter:	acc_dtype - The dtype of the internal accumulator. If None (default), we use the dtype in the list below, or the input dtype if its precision is higher: for int dtypes, we use at least int64; for uint dtypes, we use at least uint64; for float dtypes, we use at least float64; for complex dtypes, we use at least complex128.
Returns:	sum of x along axis

axis can be:

None - in which case the sum is computed along all axes (like numpy)
an int - computed along this axis
a list of ints - computed along these axes

theano.tensor.prod(x, axis=None, dtype=None, keepdims=False, acc_dtype=None, no_zeros_in_input=False)¶

Parameter:	x - symbolic Tensor (or compatible)
Parameter:	axis - axis or axes along which to compute the product
Parameter:	dtype - The dtype of the returned tensor. If None, then we use the default dtype which is the same as the input tensor’s dtype except when: the input dtype is a signed integer of precision < 64 bit, in which case we use int64 the input dtype is an unsigned integer of precision < 64 bit, in which case we use uint64 This default dtype does _not_ depend on the value of “acc_dtype”.
Parameter:	keepdims - (boolean) If this is set to True, the axes which are reduced are left in the result as dimensions with size one. With this option, the result will broadcast correctly against the original tensor.
Parameter:	acc_dtype - The dtype of the internal accumulator. If None (default), we use the dtype in the list below, or the input dtype if its precision is higher: for int dtypes, we use at least int64; for uint dtypes, we use at least uint64; for float dtypes, we use at least float64; for complex dtypes, we use at least complex128.
Parameter:	no_zeros_in_input - The grad of prod is complicated as we need to handle 3 different cases: without zeros in the input reduced group, with 1 zero or with more zeros. This could slow you down, but more importantly, we currently don’t support the second derivative of the 3 cases. So you cannot take the second derivative of the default prod(). To remove the handling of the special cases of 0 and so get some small speed up and allow second derivative set `no_zeros_in_inputs` to `True`. It defaults to `False`. It is the user responsibility to make sure there are no zeros in the inputs. If there are, the grad will be wrong.
Returns:	product of every term in x along axis

axis can be:

None - in which case the sum is computed along all axes (like numpy)
an int - computed along this axis
a list of ints - computed along these axes

theano.tensor.mean(x, axis=None, dtype=None, keepdims=False, acc_dtype=None)¶

Parameter:	x - symbolic Tensor (or compatible)
Parameter:	axis - axis or axes along which to compute the mean
Parameter:	dtype - The dtype to cast the result of the inner summation into. For instance, by default, a sum of a float32 tensor will be done in float64 (acc_dtype would be float64 by default), but that result will be casted back in float32.
Parameter:	keepdims - (boolean) If this is set to True, the axes which are reduced are left in the result as dimensions with size one. With this option, the result will broadcast correctly against the original tensor.
Parameter:	acc_dtype - The dtype of the internal accumulator of the inner summation. This will not necessarily be the dtype of the output (in particular if it is a discrete (int/uint) dtype, the output will be in a float type). If None, then we use the same rules as `sum()`.
Returns:	mean value of x along axis

axis can be:

None - in which case the mean is computed along all axes (like numpy)
an int - computed along this axis
a list of ints - computed along these axes

theano.tensor.var(x, axis=None, keepdims=False)¶

Parameter:	x - symbolic Tensor (or compatible)
Parameter:	axis - axis or axes along which to compute the variance
Parameter:	keepdims - (boolean) If this is set to True, the axes which are reduced are left in the result as dimensions with size one. With this option, the result will broadcast correctly against the original tensor.
Returns:	variance of x along axis

axis can be:

None - in which case the variance is computed along all axes (like numpy)
an int - computed along this axis
a list of ints - computed along these axes

theano.tensor.std(x, axis=None, keepdims=False)¶

Parameter:	x - symbolic Tensor (or compatible)
Parameter:	axis - axis or axes along which to compute the standard deviation
Parameter:	keepdims - (boolean) If this is set to True, the axes which are reduced are left in the result as dimensions with size one. With this option, the result will broadcast correctly against the original tensor.
Returns:	variance of x along axis

axis can be:

None - in which case the standard deviation is computed along all axes (like numpy)
an int - computed along this axis
a list of ints - computed along these axes

theano.tensor.all(x, axis=None, keepdims=False)¶

Parameter:	x - symbolic Tensor (or compatible)
Parameter:	axis - axis or axes along which to apply ‘bitwise and’
Parameter:	keepdims - (boolean) If this is set to True, the axes which are reduced are left in the result as dimensions with size one. With this option, the result will broadcast correctly against the original tensor.
Returns:	bitwise and of x along axis

axis can be:

None - in which case the ‘bitwise and’ is computed along all axes (like numpy)
an int - computed along this axis
a list of ints - computed along these axes

theano.tensor.any(x, axis=None, keepdims=False)¶

Parameter:	x - symbolic Tensor (or compatible)
Parameter:	axis - axis or axes along which to apply bitwise or
Parameter:	keepdims - (boolean) If this is set to True, the axes which are reduced are left in the result as dimensions with size one. With this option, the result will broadcast correctly against the original tensor.
Returns:	bitwise or of x along axis

axis can be:

None - in which case the ‘bitwise or’ is computed along all axes (like numpy)
an int - computed along this axis
a list of ints - computed along these axes

theano.tensor.ptp(x, axis = None)¶

Range of values (maximum - minimum) along an axis. The name of the function comes from the acronym for peak to peak.

Parameter:	x Input tensor.
Parameter:	axis Axis along which to find the peaks. By default, flatten the array.
Returns:	A new array holding the result.

Indexing¶

Like NumPy, Theano distinguishes between basic and advanced indexing. Theano fully supports basic indexing (see NumPy’s indexing).

Integer advanced indexing will be supported in 0.6rc4 (or the development version). We do not support boolean masks, as Theano does not have a boolean type (we use int8 for the output of logic operators).

NumPy with a mask:

>>> n = np.arange(9).reshape(3,3)
>>> n[n > 4]
array([5, 6, 7, 8])

Theano indexing with a “mask” (incorrect approach):

>>> t = theano.tensor.arange(9).reshape((3,3))
>>> t[t > 4].eval()  # an array with shape (3, 3, 3)
array([[[0, 1, 2],
        [0, 1, 2],
        [0, 1, 2]],

       [[0, 1, 2],
        [0, 1, 2],
        [3, 4, 5]],

       [[3, 4, 5],
        [3, 4, 5],
        [3, 4, 5]]])

Getting a Theano result like NumPy:

>>> t[(t > 4).nonzero()].eval()
array([5, 6, 7, 8])

The gradient of Advanced indexing needs in many cases NumPy 1.8. It is not released yet as of April 30th, 2013. You can use NumPy development version to have this feature now.

Index-assignment is not supported. If you want to do something like a[5] = b or a[5]+=b, see theano.tensor.set_subtensor() and theano.tensor.inc_subtensor() below.

theano.tensor.set_subtensor(x, y, inplace=False, tolerate_inplace_aliasing=False)¶

Return x with the given subtensor overwritten by y.

Parameters:	x – Symbolic variable for the lvalue of = operation. y – Symbolic variable for the rvalue of = operation. tolerate_inplace_aliasing – See inc_subtensor for documentation.

Examples

To replicate the numpy expression “r[10:] = 5”, type

>>> r = ivector()
>>> new_r = set_subtensor(r[10:], 5)

theano.tensor.inc_subtensor(x, y, inplace=False, set_instead_of_inc=False, tolerate_inplace_aliasing=False)¶

Return x with the given subtensor incremented by y.

Parameters:

x – The symbolic result of a Subtensor operation.
y – The amount by which to increment the subtensor in question.
inplace – Don’t use. Theano will do it when possible.
set_instead_of_inc – If True, do a set_subtensor instead.
tolerate_inplace_aliasing – Allow x and y to be views of a single underlying array even while working inplace. For correct results, x and y must not be overlapping views; if they overlap, the result of this Op will generally be incorrect. This value has no effect if inplace=False.

Examples

To replicate the numpy expression “r[10:] += 5”, type

>>> r = ivector()
>>> new_r = inc_subtensor(r[10:], 5)

Operator Support¶

Many Python operators are supported.

>>> a, b = T.itensor3(), T.itensor3() # example inputs

Arithmetic¶

>>> a + 3      # T.add(a, 3) -> itensor3
>>> 3 - a      # T.sub(3, a)
>>> a * 3.5    # T.mul(a, 3.5) -> ftensor3 or dtensor3 (depending on casting)
>>> 2.2 / a    # T.truediv(2.2, a)
>>> 2.2 // a   # T.intdiv(2.2, a)
>>> 2.2**a     # T.pow(2.2, a)
>>> b % a      # T.mod(b, a)

Bitwise¶

>>> a & b      # T.and_(a,b)    bitwise and (alias T.bitwise_and)
>>> a ^ 1      # T.xor(a,1)     bitwise xor (alias T.bitwise_xor)
>>> a | b      # T.or_(a,b)     bitwise or (alias T.bitwise_or)
>>> ~a         # T.invert(a)    bitwise invert (alias T.bitwise_not)

Inplace¶

In-place operators are not supported. Theano’s graph-optimizations will determine which intermediate values to use for in-place computations. If you would like to update the value of a shared variable, consider using the updates argument to theano.function().

Elementwise¶

Casting¶

theano.tensor.cast(x, dtype)¶

Cast any tensor x to a Tensor of the same shape, but with a different numerical type dtype.

This is not a reinterpret cast, but a coersion cast, similar to numpy.asarray(x, dtype=dtype).

import theano.tensor as T
x = T.matrix()
x_as_int = T.cast(x, 'int32')

Attempting to casting a complex value to a real value is ambiguous and will raise an exception. Use real(), imag(), abs(), or angle().

theano.tensor.real(x)¶: Return the real (not imaginary) components of Tensor x. For non-complex x this function returns x.

theano.tensor.imag(x)¶: Return the imaginary components of Tensor x. For non-complex x this function returns zeros_like(x).

Comparisons¶

The six usual equality and inequality operators share the same interface.

Parameter:	a - symbolic Tensor (or compatible)
Parameter:	b - symbolic Tensor (or compatible)
Return type:	symbolic Tensor
Returns:	a symbolic tensor representing the application of the logical elementwise operator.

Note

Theano has no boolean dtype. Instead, all boolean tensors are represented in 'int8'.

Here is an example with the less-than operator.

import theano.tensor as T
x,y = T.dmatrices('x','y')
z = T.le(x,y)

theano.tensor.lt(a, b)¶

Returns a symbolic 'int8' tensor representing the result of logical less-than (a<b).

Also available using syntax a < b

theano.tensor.gt(a, b)¶

Returns a symbolic 'int8' tensor representing the result of logical greater-than (a>b).

Also available using syntax a > b

theano.tensor.le(a, b)¶

Returns a variable representing the result of logical less than or equal (a<=b).

Also available using syntax a <= b

theano.tensor.ge(a, b)¶

Returns a variable representing the result of logical greater or equal than (a>=b).

Also available using syntax a >= b

theano.tensor.eq(a, b)¶: Returns a variable representing the result of logical equality (a==b).

theano.tensor.neq(a, b)¶: Returns a variable representing the result of logical inequality (a!=b).

theano.tensor.isnan(a)¶

Returns a variable representing the comparison of a elements with nan.

This is equivalent to numpy.isnan.

theano.tensor.isinf(a)¶

Returns a variable representing the comparison of a elements with inf or -inf.

This is equivalent to numpy.isinf.

theano.tensor.isclose(a, b, rtol=1e-05, atol=1e-08, equal_nan=False)¶

Returns a symbolic 'int8' tensor representing where two tensors are equal within a tolerance.

The tolerance values are positive, typically very small numbers. The relative difference (rtol * abs(b)) and the absolute difference atol are added together to compare against the absolute difference between a and b.

For finite values, isclose uses the following equation to test whether two floating point values are equivalent: |a - b| <= (atol + rtol * |b|)

For infinite values, isclose checks if both values are the same signed inf value.

If equal_nan is True, isclose considers NaN values in the same position to be close. Otherwise, NaN values are not considered close.

This is equivalent to numpy.isclose.

theano.tensor.allclose(a, b, rtol=1e-05, atol=1e-08, equal_nan=False)¶

Returns a symbolic 'int8' value representing if all elements in two tensors are equal within a tolerance.

See notes in isclose for determining values equal within a tolerance.

This is equivalent to numpy.allclose.

Condition¶

theano.tensor.switch(cond, ift, iff)¶

Returns a variable representing a switch between ift (iftrue) and iff (iffalse)

based on the condition cond. This is the theano equivalent of numpy.where.

Parameter: cond - symbolic Tensor (or compatible)

Parameter: ift - symbolic Tensor (or compatible)

Parameter: iff - symbolic Tensor (or compatible)

Return type: symbolic Tensor

import theano.tensor as T
a,b = T.dmatrices('a','b')
x,y = T.dmatrices('x','y')
z = T.switch(T.lt(a,b), x, y)

theano.tensor.where(cond, ift, iff)¶: Alias for switch. where is the numpy name.

theano.tensor.clip(x, min, max)¶

Return a variable representing x, but with all elements greater than max clipped to max and all elements less than min clipped to min.

Normal broadcasting rules apply to each of x, min, and max.

Bit-wise¶

The bitwise operators possess this interface:

Parameter:	a - symbolic Tensor of integer type.
Parameter:	b - symbolic Tensor of integer type.

Note

The bitwise operators must have an integer type as input.

The bit-wise not (invert) takes only one parameter.

Return type:	symbolic Tensor with corresponding dtype.

theano.tensor.and_(a, b)¶: Returns a variable representing the result of the bitwise and.

theano.tensor.or_(a, b)¶: Returns a variable representing the result of the bitwise or.

theano.tensor.xor(a, b)¶: Returns a variable representing the result of the bitwise xor.

theano.tensor.invert(a)¶: Returns a variable representing the result of the bitwise not.

theano.tensor.bitwise_and(a, b)¶: Alias for and_. bitwise_and is the numpy name.

theano.tensor.bitwise_or(a, b)¶: Alias for or_. bitwise_or is the numpy name.

theano.tensor.bitwise_xor(a, b)¶: Alias for xor_. bitwise_xor is the numpy name.

theano.tensor.bitwise_not(a, b)¶: Alias for invert. invert is the numpy name.

Here is an example using the bit-wise and_ via the & operator:

import theano.tensor as T
x,y = T.imatrices('x','y')
z = x & y

Mathematical¶

theano.tensor.abs_(a)¶: Returns a variable representingthe absolute of a, ie |a|.

Note

Can also be accessed with abs(a).

theano.tensor.angle(a)¶: Returns a variable representing angular component of complex-valued Tensor a.

theano.tensor.exp(a)¶: Returns a variable representing the exponential of a, ie e^a.

theano.tensor.maximum(a, b)¶: Returns a variable representing the maximum element by element of a and b

theano.tensor.minimum(a, b)¶: Returns a variable representing the minimum element by element of a and b

theano.tensor.neg(a)¶: Returns a variable representing the negation of a (also -a).

theano.tensor.inv(a)¶: Returns a variable representing the inverse of a, ie 1.0/a. Also called reciprocal.

theano.tensor.log(a), log2(a), log10(a)¶: Returns a variable representing the base e, 2 or 10 logarithm of a.

theano.tensor.sgn(a)¶: Returns a variable representing the sign of a.

theano.tensor.ceil(a)¶: Returns a variable representing the ceiling of a (for example ceil(2.1) is 3).

theano.tensor.floor(a)¶: Returns a variable representing the floor of a (for example floor(2.9) is 2).

theano.tensor.round(a, mode="half_away_from_zero")¶: Returns a variable representing the rounding of a in the same dtype as a. Implemented rounding mode are half_away_from_zero and half_to_even.

theano.tensor.iround(a, mode="half_away_from_zero")¶: Short hand for cast(round(a, mode),’int64’).

theano.tensor.sqr(a)¶: Returns a variable representing the square of a, ie a^2.

theano.tensor.sqrt(a)¶: Returns a variable representing the of a, ie a^0.5.

theano.tensor.cos(a), sin(a), tan(a)¶: Returns a variable representing the trigonometric functions of a (cosine, sine and tangent).

theano.tensor.cosh(a), sinh(a), tanh(a)¶: Returns a variable representing the hyperbolic trigonometric functions of a (hyperbolic cosine, sine and tangent).

theano.tensor.erf(a), erfc(a)¶: Returns a variable representing the error function or the complementary error function. wikipedia

theano.tensor.erfinv(a), erfcinv(a)¶: Returns a variable representing the inverse error function or the inverse complementary error function. wikipedia

theano.tensor.gamma(a)¶: Returns a variable representing the gamma function.

theano.tensor.gammaln(a)¶: Returns a variable representing the logarithm of the gamma function.

theano.tensor.psi(a)¶: Returns a variable representing the derivative of the logarithm of the gamma function (also called the digamma function).

theano.tensor.chi2sf(a, df)¶

Returns a variable representing the survival function (1-cdf — sometimes more accurate).

C code is provided in the Theano_lgpl repository. This makes it faster.

https://github.com/Theano/Theano_lgpl.git

Broadcasting in Theano vs. Numpy¶

Broadcasting is a mechanism which allows tensors with different numbers of dimensions to be added or multiplied together by (virtually) replicating the smaller tensor along the dimensions that it is lacking.

Broadcasting is the mechanism by which a scalar may be added to a matrix, a vector to a matrix or a scalar to a vector.

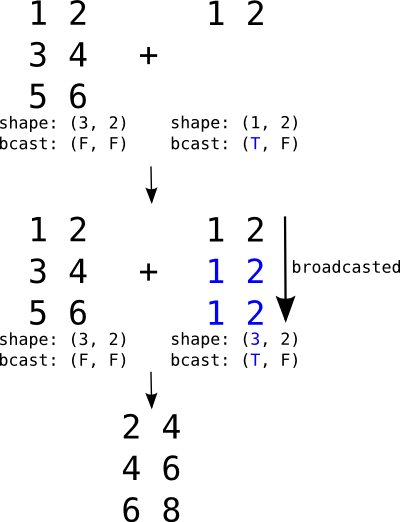
Broadcasting a row matrix. T and F respectively stand for True and False and indicate along which dimensions we allow broadcasting.

If the second argument were a vector, its shape would be (2,) and its broadcastable pattern (F,). They would be automatically expanded to the left to match the dimensions of the matrix (adding 1 to the shape and T to the pattern), resulting in (1, 2) and (T, F). It would then behave just like the example above.

Unlike numpy which does broadcasting dynamically, Theano needs to know, for any operation which supports broadcasting, which dimensions will need to be broadcasted. When applicable, this information is given in the Type of a Variable.

Linear Algebra¶

theano.tensor.dot(X, Y)¶

For 2-D arrays it is equivalent to matrix multiplication, and for 1-D arrays to inner product of vectors (without complex conjugation). For N dimensions it is a sum product over the last axis of a and the second-to-last of b:

Parameters:	X (symbolic tensor) – left term Y (symbolic tensor) – right term
Return type:	symbolic matrix or vector
Returns:	the inner product of X and Y.

theano.tensor.outer(X, Y)¶

Parameters:	X (symbolic vector) – left term Y (symbolic vector) – right term
Return type:	symbolic matrix
Returns:	vector-vector outer product

theano.tensor.tensordot(a, b, axes=2)¶

Given two tensors a and b,tensordot computes a generalized dot product over the provided axes. Theano’s implementation reduces all expressions to matrix or vector dot products and is based on code from Tijmen Tieleman’s gnumpy (http://www.cs.toronto.edu/~tijmen/gnumpy.html).

Parameters:	a (symbolic tensor) – the first tensor variable b (symbolic tensor) – the second tensor variable axes (int or array-like of length 2) – an integer or array. If an integer, the number of axes to sum over. If an array, it must have two array elements containing the axes to sum over in each tensor. Note that the default value of 2 is not guaranteed to work for all values of a and b, and an error will be raised if that is the case. The reason for keeping the default is to maintain the same signature as numpy’s tensordot function (and np.tensordot raises analogous errors for non-compatible inputs). If an integer i, it is converted to an array containing the last i dimensions of the first tensor and the first i dimensions of the second tensor: axes = [range(a.ndim - i, b.ndim), range(i)] If an array, its two elements must contain compatible axes of the two tensors. For example, [[1, 2], [2, 0]] means sum over the 2nd and 3rd axes of a and the 3rd and 1st axes of b. (Remember axes are zero-indexed!) The 2nd axis of a and the 3rd axis of b must have the same shape; the same is true for the 3rd axis of a and the 1st axis of b.
Returns:	a tensor with shape equal to the concatenation of a’s shape (less any dimensions that were summed over) and b’s shape (less any dimensions that were summed over).
Return type:	symbolic tensor

It may be helpful to consider an example to see what tensordot does. Theano’s implementation is identical to NumPy’s. Here a has shape (2, 3, 4) and b has shape (5, 6, 4, 3). The axes to sum over are [[1, 2], [3, 2]] – note that a.shape[1] == b.shape[3] and a.shape[2] == b.shape[2]; these axes are compatible. The resulting tensor will have shape (2, 5, 6) – the dimensions that are not being summed:

import numpy as np

a = np.random.random((2,3,4))
b = np.random.random((5,6,4,3))

#tensordot
c = np.tensordot(a, b, [[1,2],[3,2]])

#loop replicating tensordot
a0, a1, a2 = a.shape
b0, b1, _, _ = b.shape
cloop = np.zeros((a0,b0,b1))

#loop over non-summed indices -- these exist
#in the tensor product.
for i in range(a0):
    for j in range(b0):
        for k in range(b1):
            #loop over summed indices -- these don't exist
            #in the tensor product.
            for l in range(a1):
                for m in range(a2):
                    cloop[i,j,k] += a[i,l,m] * b[j,k,m,l]

assert np.allclose(c, cloop)

This specific implementation avoids a loop by transposing a and b such that the summed axes of a are last and the summed axes of b are first. The resulting arrays are reshaped to 2 dimensions (or left as vectors, if appropriate) and a matrix or vector dot product is taken. The result is reshaped back to the required output dimensions.

In an extreme case, no axes may be specified. The resulting tensor will have shape equal to the concatenation of the shapes of a and b:

>>> c = np.tensordot(a, b, 0)
>>> a.shape
(2, 3, 4)
>>> b.shape
(5, 6, 4, 3)
>>> print(c.shape)
(2, 3, 4, 5, 6, 4, 3)

Note:	See the documentation of numpy.tensordot for more examples.

theano.tensor.batched_dot(X, Y)¶

Parameters:	x – A Tensor with sizes e.g.: for 3D (dim1, dim3, dim2) y – A Tensor with sizes e.g.: for 3D (dim1, dim2, dim4)

This function computes the dot product between the two tensors, by iterating over the first dimension using scan. Returns a tensor of size e.g. if it is 3D: (dim1, dim3, dim4) Example:

>>> first = T.tensor3('first')
>>> second = T.tensor3('second')
>>> result = batched_dot(first, second)

Note:	This is a subset of numpy.einsum, but we do not provide it for now. But numpy einsum is slower than dot or tensordot: http://mail.scipy.org/pipermail/numpy-discussion/2012-October/064259.html
Parameters:	X (symbolic tensor) – left term Y (symbolic tensor) – right term
Returns:	tensor of products

theano.tensor.batched_tensordot(X, Y, axes=2)¶

Parameters:	x – A Tensor with sizes e.g.: for 3D (dim1, dim3, dim2) y – A Tensor with sizes e.g.: for 3D (dim1, dim2, dim4) axes (int or array-like of length 2) – an integer or array. If an integer, the number of axes to sum over. If an array, it must have two array elements containing the axes to sum over in each tensor. If an integer i, it is converted to an array containing the last i dimensions of the first tensor and the first i dimensions of the second tensor (excluding the first (batch) dimension): axes = [range(a.ndim - i, b.ndim), range(1,i+1)] If an array, its two elements must contain compatible axes of the two tensors. For example, [[1, 2], [2, 4]] means sum over the 2nd and 3rd axes of a and the 3rd and 5th axes of b. (Remember axes are zero-indexed!) The 2nd axis of a and the 3rd axis of b must have the same shape; the same is true for the 3rd axis of a and the 5th axis of b.
Returns:	a tensor with shape equal to the concatenation of a’s shape (less any dimensions that were summed over) and b’s shape (less first dimension and any dimensions that were summed over).
Return type:	tensor of tensordots

A hybrid of batch_dot and tensordot, this function computes the tensordot product between the two tensors, by iterating over the first dimension using scan to perform a sequence of tensordots.

Note:	See `tensordot()` and `batched_dot()` for supplementary documentation.

theano.tensor.mgrid()¶

Returns:	an instance which returns a dense (or fleshed out) mesh-grid when indexed, so that each returned argument has the same shape. The dimensions and number of the output arrays are equal to the number of indexing dimensions. If the step length is not a complex number, then the stop is not inclusive.

Example:

>>> a = T.mgrid[0:5, 0:3]
>>> a[0].eval()
array([[0, 0, 0],
       [1, 1, 1],
       [2, 2, 2],
       [3, 3, 3],
       [4, 4, 4]])
>>> a[1].eval()
array([[0, 1, 2],
       [0, 1, 2],
       [0, 1, 2],
       [0, 1, 2],
       [0, 1, 2]])

theano.tensor.ogrid()¶

Returns:	an instance which returns an open (i.e. not fleshed out) mesh-grid when indexed, so that only one dimension of each returned array is greater than 1. The dimension and number of the output arrays are equal to the number of indexing dimensions. If the step length is not a complex number, then the stop is not inclusive.

Example:

>>> b = T.ogrid[0:5, 0:3]
>>> b[0].eval()
array([[0],
       [1],
       [2],
       [3],
       [4]])
>>> b[1].eval()
array([[0, 1, 2]])

Gradient / Differentiation¶

Driver for gradient calculations.

theano.gradient.grad(cost, wrt, consider_constant=None, disconnected_inputs='raise', add_names=True, known_grads=None, return_disconnected='zero', null_gradients='raise')

Return symbolic gradients for one or more variables with respect to some cost.

For more information about how automatic differentiation works in Theano, see gradient. For information on how to implement the gradient of a certain Op, see grad().

Parameters:	cost (scalar (0-dimensional) tensor variable or None) – Value with respect to which we are differentiating. May be None if known_grads is provided. wrt (variable or list of variables) – term[s] for which we want gradients consider_constant (list of variables) – expressions not to backpropagate through disconnected_inputs ({‘ignore’, ‘warn’, ‘raise’}) – Defines the behaviour if some of the variables in wrt are not part of the computational graph computing cost (or if all links are non-differentiable). The possible values are: ‘ignore’: considers that the gradient on these parameters is zero. ‘warn’: consider the gradient zero, and print a warning. ‘raise’: raise DisconnectedInputError. add_names (bool) – If True, variables generated by grad will be named (d<cost.name>/d<wrt.name>) provided that both cost and wrt have names known_grads (dict, optional) – A dictionary mapping variables to their gradients. This is useful in the case where you know the gradient on some variables but do not know the original cost. return_disconnected ({‘zero’, ‘None’, ‘Disconnected’}) – ‘zero’ : If wrt[i] is disconnected, return value i will be wrt[i].zeros_like() ‘None’ : If wrt[i] is disconnected, return value i will be None ‘Disconnected’ : returns variables of type DisconnectedType null_gradients ({‘raise’, ‘return’}) – Defines the behaviour if some of the variables in wrt have a null gradient. The possibles values are: ‘raise’ : raise a NullTypeGradError exception ‘return’ : return the null gradients
Returns:	symbolic expression of gradient of cost with respect to each of the wrt terms. If an element of wrt is not differentiable with respect to the output, then a zero variable is returned.
Return type:	variable or list/tuple of variables (matches wrt)

See the gradient page for complete documentation of the gradient module.

Table Of Contents

Previous topic

Next topic

This Page

Basic Tensor Functionality¶

Creation¶

Constructors with optional dtype¶

All Fully-Typed Constructors¶

Plural Constructors¶

Custom tensor types¶

Converting from Python Objects¶

TensorType and TensorVariable¶

TensorVariable¶

Shaping and Shuffling¶

Creating Tensor¶

Reductions¶

Indexing¶

Operator Support¶

Arithmetic¶

Bitwise¶

Inplace¶

Elementwise¶

Casting¶

Comparisons¶

Condition¶

Bit-wise¶

Mathematical¶

Broadcasting in Theano vs. Numpy¶

Linear Algebra¶

Gradient / Differentiation¶

Parameter:	cond - symbolic Tensor (or compatible)
Parameter:	ift - symbolic Tensor (or compatible)
Parameter:	iff - symbolic Tensor (or compatible)
Return type:	symbolic Tensor