tensor.nlinalg – Linear Algebra Ops Using Numpy¶
Note
This module is not imported by default. You need to import it to use it.
API¶
-
class
theano.tensor.nlinalg.AllocDiag(use_c_code='/usr/bin/g++')¶ Allocates a square matrix with the given vector as its diagonal.
-
class
theano.tensor.nlinalg.Det(use_c_code='/usr/bin/g++')¶ Matrix determinant. Input should be a square matrix.
-
class
theano.tensor.nlinalg.Eig(use_c_code='/usr/bin/g++')¶ Compute the eigenvalues and right eigenvectors of a square array.
-
class
theano.tensor.nlinalg.Eigh(UPLO='L')¶ Return the eigenvalues and eigenvectors of a Hermitian or symmetric matrix.
-
grad(inputs, g_outputs)¶ The gradient function should return
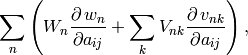
where [
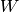 ,
, 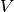 ] corresponds to
] corresponds to g_outputs, to
to inputs, and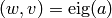 .
.Analytic formulae for eigensystem gradients are well-known in perturbation theory:
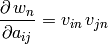
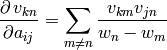
-
-
class
theano.tensor.nlinalg.EighGrad(UPLO='L')¶ Gradient of an eigensystem of a Hermitian matrix.
-
perform(node, inputs, outputs)¶ Implements the “reverse-mode” gradient for the eigensystem of a square matrix.
-
-
class
theano.tensor.nlinalg.ExtractDiag(view=False)¶ Return the diagonal of a matrix.
Notes
Works on the GPU.
-
perform(node, ins, outs)¶ For some reason numpy.diag(x) is really slow, so we implemented our own.
-
-
class
theano.tensor.nlinalg.MatrixInverse¶ Computes the inverse of a matrix
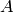 .
.Given a square matrix
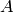 ,
, matrix_inversereturns a square matrix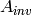 such that the dot product
such that the dot product  and
and 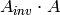 equals the identity matrix
equals the identity matrix 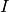 .
.Notes
When possible, the call to this op will be optimized to the call of
solve.-
R_op(inputs, eval_points)¶ The gradient function should return
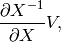
where
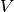 corresponds to
corresponds to g_outputsand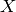 to
to
inputs. Using the matrix cookbook, one can deduce that the relation corresponds to
-
grad(inputs, g_outputs)¶ The gradient function should return
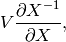
where
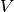 corresponds to
corresponds to g_outputsand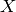 to
to
inputs. Using the matrix cookbook, one can deduce that the relation corresponds to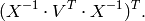
-
-
class
theano.tensor.nlinalg.MatrixPinv¶ Computes the pseudo-inverse of a matrix
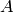 .
.The pseudo-inverse of a matrix
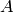 , denoted
, denoted 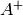 , is
defined as: “the matrix that ‘solves’ [the least-squares problem]
, is
defined as: “the matrix that ‘solves’ [the least-squares problem]
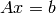 ,” i.e., if
,” i.e., if 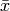 is said solution, then
is said solution, then
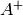 is that matrix such that
is that matrix such that 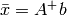 .
.Note that
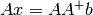 , so
, so 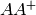 is close to the identity matrix.
This method is not faster than matrix_inverse. Its strength comes from
that it works for non-square matrices.
If you have a square matrix though, matrix_inverse can be both more
exact and faster to compute. Also this op does not get optimized into a
solve op.
is close to the identity matrix.
This method is not faster than matrix_inverse. Its strength comes from
that it works for non-square matrices.
If you have a square matrix though, matrix_inverse can be both more
exact and faster to compute. Also this op does not get optimized into a
solve op.
-
class
theano.tensor.nlinalg.QRFull(mode)¶ Full QR Decomposition.
Computes the QR decomposition of a matrix. Factor the matrix a as qr, where q is orthonormal and r is upper-triangular.
-
class
theano.tensor.nlinalg.QRIncomplete(mode)¶ Incomplete QR Decomposition.
Computes the QR decomposition of a matrix. Factor the matrix a as qr and return a single matrix.
-
class
theano.tensor.nlinalg.SVD(full_matrices=True, compute_uv=True)¶ Parameters: - full_matrices (bool, optional) – If True (default), u and v have the shapes (M, M) and (N, N), respectively. Otherwise, the shapes are (M, K) and (K, N), respectively, where K = min(M, N).
- compute_uv (bool, optional) – Whether or not to compute u and v in addition to s. True by default.
-
theano.tensor.nlinalg.diag(x)¶ Numpy-compatibility method If x is a matrix, return its diagonal. If x is a vector return a matrix with it as its diagonal.
- This method does not support the k argument that numpy supports.
-
theano.tensor.nlinalg.matrix_dot(*args)¶ Shorthand for product between several dots.
Given
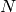 matrices
matrices 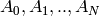 ,
, matrix_dotwill generate the matrix product between all in the given order, namely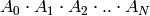 .
.
-
theano.tensor.nlinalg.qr(a, mode='full')¶ Computes the QR decomposition of a matrix. Factor the matrix a as qr, where q is orthonormal and r is upper-triangular.
Parameters: - a (array_like, shape (M, N)) – Matrix to be factored.
- mode ({‘reduced’, ‘complete’, ‘r’, ‘raw’, ‘full’, ‘economic’}, optional) –
If K = min(M, N), then
- ‘reduced’
- returns q, r with dimensions (M, K), (K, N)
- ‘complete’
- returns q, r with dimensions (M, M), (M, N)
- ‘r’
- returns r only with dimensions (K, N)
- ‘raw’
- returns h, tau with dimensions (N, M), (K,)
- ‘full’
- alias of ‘reduced’, deprecated (default)
- ‘economic’
- returns h from ‘raw’, deprecated.
The options ‘reduced’, ‘complete’, and ‘raw’ are new in numpy 1.8, see the notes for more information. The default is ‘reduced’ and to maintain backward compatibility with earlier versions of numpy both it and the old default ‘full’ can be omitted. Note that array h returned in ‘raw’ mode is transposed for calling Fortran. The ‘economic’ mode is deprecated. The modes ‘full’ and ‘economic’ may be passed using only the first letter for backwards compatibility, but all others must be spelled out.
Default mode is ‘full’ which is also default for numpy 1.6.1.
note: Default mode was left to full as full and reduced are both doing the same thing in the new numpy version but only full works on the old previous numpy version.
Returns: - q (matrix of float or complex, optional) – A matrix with orthonormal columns. When mode = ‘complete’ the result is an orthogonal/unitary matrix depending on whether or not a is real/complex. The determinant may be either +/- 1 in that case.
- r (matrix of float or complex, optional) – The upper-triangular matrix.
-
theano.tensor.nlinalg.svd(a, full_matrices=1, compute_uv=1)¶ This function performs the SVD on CPU.
Parameters: - full_matrices (bool, optional) – If True (default), u and v have the shapes (M, M) and (N, N), respectively. Otherwise, the shapes are (M, K) and (K, N), respectively, where K = min(M, N).
- compute_uv (bool, optional) – Whether or not to compute u and v in addition to s. True by default.
Returns: U, V, D
Return type: matrices
-
theano.tensor.nlinalg.trace(X)¶ Returns the sum of diagonal elements of matrix X.
Notes
Works on GPU since 0.6rc4.
