Word2Vec: Obtain word embeddings¶
0. Introduction¶
Word2vec is the tool for generating the distributed representation of words, which is proposed by Mikolov et al[1]. When the tool assigns a real-valued vector to each word, the closer the meanings of the words, the greater similarity the vectors will indicate.
Distributed representation means assigning a real-valued vector for each word and representing the word by the vector. When representing a word by distributed representation, we call the word embeddings. In this tutorial, we aim at explaining how to get the word embeddings from Penn Tree Bank dataset.
Let’s think about what the meaning of word is. Since we are human, we can understand that the words “animal” and “dog” are deeply related each other. But what information will Word2vec use to learn the vectors for words? The words “animal” and “dog” should have similar vectors, but the words “food” and “dog” should be far from each other. How to know the features of those words automatically?
1. Basic Idea¶
Word2vec learns the similarity of word meanings from simple information. It learns the representation of words from sentences. The core idea is based on the assumption that the meaning of a word is affected by the words around it. This idea follows distributional hypothesis[2].
The word we focus on to learn its representation is called center word, and the words around it are called context words. The window size \(C\) determines the number of context words which is considered.
Here, let’s see the algorithm by using an example sentence: “The cute cat jumps over the lazy dog.”.
All of the following figures consider “cat” as the center word.
According to the window size \(C\), you can see that the number of context words is changed.

2. Main Algorithm¶
Word2vec, the tool for creating the word embeddings, is actually built with two models, which are called Skip-gram and CBoW.
To explain the models with the figures below, we will use the following symbols.
Symbol |
Definition |
|---|---|
\(|\mathcal{V}|\) |
The size of vocabulary |
\(D\) |
The size of embedding vector |
\({\bf v}_t\) |
A one-hot center word vector |
\(V_{t \pm C}\) |
A set of \(2C\) context vectors around \({\bf v}_t\), namely, \(\{{\bf v}_{t+c}\}_{c=-C}^C \backslash {\bf v}_t\) |
\({\bf l}_H\) |
An embedding vector of an input word vector |
\({\bf l}_O\) |
An output vector of the network |
\({\bf W}_H\) |
The embedding matrix for inputs |
\({\bf W}_O\) |
The embedding matrix for outputs |
Note
Using negative sampling or hierarchical softmax for the loss function is very common, however, in this tutorial, we will use the softmax over all words and skip the other variants for the sake of simplicity.
2.1 Skip-gram¶
This model learns to predict context words \(V_{t \pm C}\) when a center word \({\bf v}_t\) is given. In the model, each row of the embedding matrix for input \({\bf W}_H\) becomes a word embedding of each word.
When you input a center word \({\bf v}_t\) into the network, you can predict one of context words \(\hat {\bf v}_{t+c} \in V_{t \pm C}\) as follows:
Calculate an embedding vector of the input center word vector: \({\bf l}_H = {\bf W}_H {\bf v}_t\)
Calculate an output vector of the embedding vector: \({\bf l}_O = {\bf W}_O {\bf l}_H\)
Calculate a probability vector of a context word: \(\hat {\bf v}_{t+c} = \text{softmax}({\bf l}_O)\)
Each element of the \(|\mathcal{V}|\)-dimensional vector \(\hat {\bf v}_{t+c}\) is a probability that a word in the vocabulary turns out to be a context word at position \(c\). So, the probability \(p({\bf v}_{t+c}|{\bf v}_t)\) can be estimated by a dot product of the one-hot vector \({\bf v}_{t+c}\) which represents the actual word at the position \(c\) and the output vector \(\hat {\bf v}_{t+c}\).
The loss function to predict all the context words \(V_{t \pm C}\) given a center word \({\bf v}_t\) is defined as follows:
2.2 Continuous Bag of Words (CBoW)¶
This model learns to predict center word \({\bf v}_t\) when context words \(V_{t \pm C}\) is given. When you give a set of context words \(V_{t \pm C}\) to the network, you can estimate the probability of the center word \(\hat {\bf v}_t\) as follows:
Calculate a mean embedding vector over all context words: \({\bf l}_H = \frac{1}{2C} \sum_{V_{t \pm C}} {\bf W}_H {\bf v}_{t+c}\)
Calculate an output vector of the embedding vector: \({\bf l}_O = {\bf W}_O {\bf l}_H\)
Calculate a probability vector of a center word: \(\hat {\bf v}_t = \text{softmax}({\bf l}_O)\)
Each element of the \(|\mathcal{V}|\)-dimensional vector \(\hat {\bf v}_t\) is a probability that a word in the vocabulary turns out to be a center word. So, the probability \(p({\bf v}_t|V_{t \pm C})\) can be estimated by a dot product of the one-hot vector \({\bf v}_t\) which represents the actual center word and the output vector \(\hat {\bf v}_t\).
The loss function to predict the center word \({\bf v}_t\) given context words \(V_{t \pm C}\) is defined as follows:
3. Details of Skip-gram¶
In this tutorial, we mainly explain Skip-gram model because
It is easier to understand the algorithm than CBoW.
Even if the number of words increases, the accuracy is largely maintained. So, it is more scalable.
So, let’s think about a concrete example of calculating Skip-gram under this setup:
The size of vocabulary \(|\mathcal{V}|\) is 10.
The size of embedding vector \(D\) is 2.
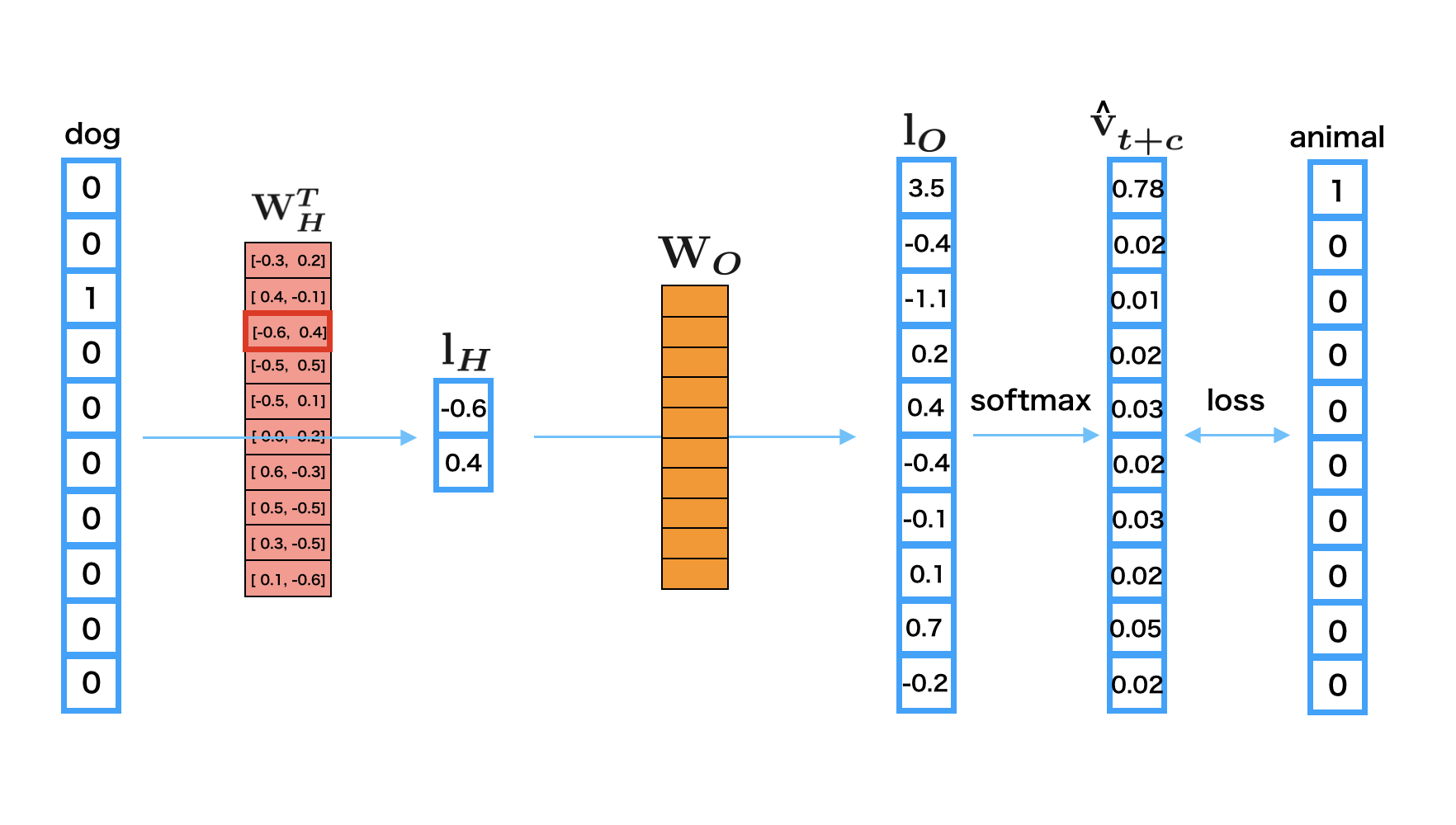
Center word is “dog”.
Context word is “animal”.
Since there should be more than one context word, repeat the following process for each context word.
The one-hot vector of “dog” is
[0 0 1 0 0 0 0 0 0 0]and you input it as the center word.The third row of embedding matrix \({\bf W}_H\) is used for the word embedding of “dog” \({\bf l}_H\).
Then, multiply \({\bf W}_O\) with \({\bf l}_H\) to obtain the output vector \({\bf l}_O\).
Give \({\bf l}_O\) to the softmax function to make it a predicted probability vector \(\hat {\bf v}_{t+c}\) for a context word at the position \(c\).
Calculate the error between \(\hat {\bf v}_{t+c}\) and the one-hot vector of “animal”;
[1 0 0 0 0 0 0 0 0 0 0].Propagate the error back to the network to update the parameters.
4. Implementation of Skip-gram in Chainer¶
There is an example of Word2vec in the official repository of Chainer, so we will explain how to implement Skip-gram based on this: examples/word2vec
4.1 Preparation¶
First, let’s import necessary packages:
import argparse
import collections
import numpy as np
import six
import chainer
from chainer.backends import cuda
import chainer.functions as F
import chainer.initializers as I
import chainer.links as L
import chainer.optimizers as O
from chainer import reporter
from chainer import training
from chainer.training import extensions
4.2 Define a Skip-gram model¶
Next, let’s define a network for Skip-gram.
class SkipGram(chainer.Chain):
"""Definition of Skip-gram Model"""
def __init__(self, n_vocab, n_units, loss_func):
super(SkipGram, self).__init__()
with self.init_scope():
self.embed = L.EmbedID(
n_vocab, n_units, initialW=I.Uniform(1. / n_units))
self.loss_func = loss_func
def forward(self, x, contexts):
e = self.embed(contexts)
batch_size, n_context, n_units = e.shape
x = F.broadcast_to(x[:, None], (batch_size, n_context))
e = F.reshape(e, (batch_size * n_context, n_units))
x = F.reshape(x, (batch_size * n_context,))
loss = self.loss_func(e, x)
reporter.report({'loss': loss}, self)
return loss
class SoftmaxCrossEntropyLoss(chainer.Chain):
"""Softmax cross entropy loss function preceded by linear transformation.
"""
def __init__(self, n_in, n_out):
super(SoftmaxCrossEntropyLoss, self).__init__()
with self.init_scope():
self.out = L.Linear(n_in, n_out, initialW=0)
def forward(self, x, t):
return F.softmax_cross_entropy(self.out(x), t)
Note
The weight matrix
self.embed.Wis the embedding matrix for input vectorx.The function call
forwardtakes the word ID of a center wordxand word IDs of context words contexts as inputs, and outputs the error calculated by the loss functionloss_funcs.t.SoftmaxCrossEntropyLoss.Note that the initial shape of
xand contexts are(batch_size,)and(batch_size, n_context), respectively.The
batch_sizemeans the size of mini-batch, andn_contextmeans the number of context words.
First, we obtain the embedding vectors of contexts by e = self.embed(contexts).
Then F.broadcast_to(x[:, None], (batch_size, n_context)) performs broadcasting of
x (its shape is (batch_size,)) to (batch_size, n_context) by copying the
same value n_context time to fill the second axis, and then the broadcasted x
is reshaped into 1-D vector (batchsize * n_context,) while e is reshaped to
(batch_size * n_context, n_units).
In Skip-gram model, predicting a context word from the center word is the same as
predicting the center word from a context word because the center word is always
a context word when considering the context word as a center word. So, we create
batch_size * n_context center word predictions by applying self.out linear
layer to the embedding vectors of context words. Then, calculate softmax cross
entropy between the broadcasted center word ID x and the predictions.
4.3 Prepare dataset and iterator¶
Let’s retrieve the Penn Tree Bank (PTB) dataset by using Chainer’s dataset utility
get_ptb_words() method.
train, val, _ = chainer.datasets.get_ptb_words()
counts = collections.Counter(train)
Then define an iterator to make mini-batches that contain a set of center words with their context words.
train and val means training data and validation data. Each data contains
the list of Document IDs:
>>> train array([ 0, 1, 2, ..., 39, 26, 24], dtype=int32) >>> val array([2211, 396, 1129, ..., 108, 27, 24], dtype=int32)
class WindowIterator(chainer.dataset.Iterator):
"""Dataset iterator to create a batch of sequences at different positions.
This iterator returns a pair of the current words and the context words.
"""
def __init__(self, dataset, window, batch_size, repeat=True):
self.dataset = np.array(dataset, np.int32)
self.window = window # size of context window
self.batch_size = batch_size
self._repeat = repeat
# order is the array which is shuffled ``[window, window + 1, ...,
# len(dataset) - window - 1]``
self.order = np.random.permutation(
len(dataset) - window * 2).astype(np.int32)
self.order += window
self.current_position = 0
# Number of completed sweeps over the dataset. In this case, it is
# incremented if every word is visited at least once after the last
# increment.
self.epoch = 0
# True if the epoch is incremented at the last iteration.
self.is_new_epoch = False
def __next__(self):
"""This iterator returns a list representing a mini-batch.
Each item indicates a different position in the original sequence.
"""
if not self._repeat and self.epoch > 0:
raise StopIteration
i = self.current_position
i_end = i + self.batch_size
position = self.order[i:i_end]
w = np.random.randint(self.window - 1) + 1
offset = np.concatenate([np.arange(-w, 0), np.arange(1, w + 1)])
pos = position[:, None] + offset[None, :]
contexts = self.dataset.take(pos)
center = self.dataset.take(position)
if i_end >= len(self.order):
np.random.shuffle(self.order)
self.epoch += 1
self.is_new_epoch = True
self.current_position = 0
else:
self.is_new_epoch = False
self.current_position = i_end
return center, contexts
@property
def epoch_detail(self):
return self.epoch + float(self.current_position) / len(self.order)
def serialize(self, serializer):
self.current_position = serializer('current_position',
self.current_position)
self.epoch = serializer('epoch', self.epoch)
self.is_new_epoch = serializer('is_new_epoch', self.is_new_epoch)
if self._order is not None:
serializer('_order', self._order)
In the constructor, we create an array
self.orderwhich denotes shuffled indices of[window, window + 1, ..., len(dataset) - window - 1]in order to choose a center word randomly from dataset in a mini-batch.The iterator definition
__next__returnsbatch_sizesets of center word and context words.The code
self.order[i:i_end]returns the indices for a set of center words from the random-ordered arrayself.order. The center word IDs center at the random indices are retrieved byself.dataset.take.np.concatenate([np.arange(-w, 0), np.arange(1, w + 1)])creates a set of offsets to retrieve context words from the dataset.The code
position[:, None] + offset[None, :]generates the indices of context words for each center word index in position. The context word IDs context are retrieved byself.dataset.take.
4.4 Prepare model, optimizer, and updater¶
model = SkipGram(n_vocab, args.unit, loss_func)
optimizer = O.Adam()
optimizer.setup(model)
train_iter = WindowIterator(train, args.window, args.batchsize)
val_iter = WindowIterator(val, args.window, args.batchsize, repeat=False)
# Set up an updater
updater = training.updaters.StandardUpdater(
train_iter, optimizer, converter=convert, device=args.gpu)
trainer = training.Trainer(updater, (args.epoch, 'epoch'), out=args.out)
trainer.extend(extensions.Evaluator(
val_iter, model, converter=convert, device=args.gpu))
trainer.extend(extensions.LogReport())
trainer.extend(extensions.PrintReport(
['epoch', 'main/loss', 'validation/main/loss']))
trainer.extend(extensions.ProgressBar())
trainer.run()
4.5 Start training¶
$ pwd
/root2chainer/chainer/examples/word2vec
$ python train_word2vec.py --test # run by test mode. If you want to use all data, remove "--test".
GPU: -1
# unit: 100
Window: 5
Minibatch-size: 1000
# epoch: 20
Training model: skipgram
Output type: hsm
n_vocab: 10000
data length: 100
epoch main/loss validation/main/loss
1 4233.75 2495.33
2 1411.14 4990.66
3 4233.11 1247.66
4 2821.66 4990.65
5 4231.94 1247.66
6 5642.04 2495.3
7 5640.82 4990.64
8 5639.31 2495.28
9 2817.89 4990.62
10 1408.03 3742.94
11 5633.11 1247.62
12 4221.71 2495.21
13 4219.3 4990.56
14 4216.57 2495.16
15 4213.52 2495.12
16 5616.03 1247.55
17 5611.34 3742.78
18 2800.31 3742.74
19 1397.79 2494.95
20 2794.1 3742.66
4.5 Search the similar words¶
$ pwd
/root2chainer/chainer/examples/word2vec
$ python search.py
>> apple
query: apple
compaq: 0.6169619560241699
chip: 0.49579331278800964
retailer: 0.4904134273529053
maker: 0.4684058427810669
computer: 0.4652436673641205
>> animal
query: animal
beauty: 0.5680124759674072
human: 0.5404794216156006
insulin: 0.5365156531333923
cell: 0.5186758041381836
photographs: 0.5077002048492432