librosa.segment.recurrence_matrix

librosa.segment.recurrence_matrix(data, k=None, width=1, metric=’euclidean’, sym=False, sparse=False, mode=’connectivity’, bandwidth=None, axis=-1)

Compute a recurrence matrix from a data matrix.

rec[i, j] is non-zero if (data[:, i], data[:, j]) are k-nearest-neighbors and |i - j| >= width

Parameters:

data : np.ndarray

A feature matrix

k : int > 0 [scalar] or None

the number of nearest-neighbors for each sample

Default: k = 2 * ceil(sqrt(t - 2 * width + 1)), or k = 2 if t <= 2 * width + 1

width : int >= 1 [scalar]

only link neighbors (data[:, i], data[:, j]) if |i - j| >= width

metric : str

Distance metric to use for nearest-neighbor calculation.

See sklearn.neighbors.NearestNeighbors for details.

sym : bool [scalar]

set sym=True to only link mutual nearest-neighbors

sparse : bool [scalar]

if False, returns a dense type (ndarray) if True, returns a sparse type (scipy.sparse.csr_matrix)

mode : str, {‘connectivity’, ‘distance’, ‘affinity’}

If ‘connectivity’, a binary connectivity matrix is produced.

If ‘distance’, then a non-zero entry contains the distance between points.

If ‘affinity’, then non-zero entries are mapped to exp( - distance(i, j) / bandwidth) where bandwidth is as specified below.

bandwidth : None or float > 0

If using mode='affinity', this can be used to set the bandwidth on the affinity kernel.

If no value is provided, it is set automatically to the median distance between furthest nearest neighbors.

axis : int

The axis along which to compute recurrence. By default, the last index (-1) is taken.

Returns:

rec : np.ndarray or scipy.sparse.csr_matrix, [shape=(t, t)]

Recurrence matrix

See also

sklearn.neighbors.NearestNeighbors, scipy.spatial.distance.cdist, librosa.feature.stack_memory, recurrence_to_lag

Notes

This function caches at level 30.

Examples

Find nearest neighbors in MFCC space

>>> y, sr = librosa.load(librosa.util.example_audio_file())
>>> mfcc = librosa.feature.mfcc(y=y, sr=sr)
>>> R = librosa.segment.recurrence_matrix(mfcc)

Or fix the number of nearest neighbors to 5

>>> R = librosa.segment.recurrence_matrix(mfcc, k=5)

Suppress neighbors within +- 7 samples

>>> R = librosa.segment.recurrence_matrix(mfcc, width=7)

Use cosine similarity instead of Euclidean distance

>>> R = librosa.segment.recurrence_matrix(mfcc, metric='cosine')

Require mutual nearest neighbors

>>> R = librosa.segment.recurrence_matrix(mfcc, sym=True)

Use an affinity matrix instead of binary connectivity

>>> R_aff = librosa.segment.recurrence_matrix(mfcc, mode='affinity')

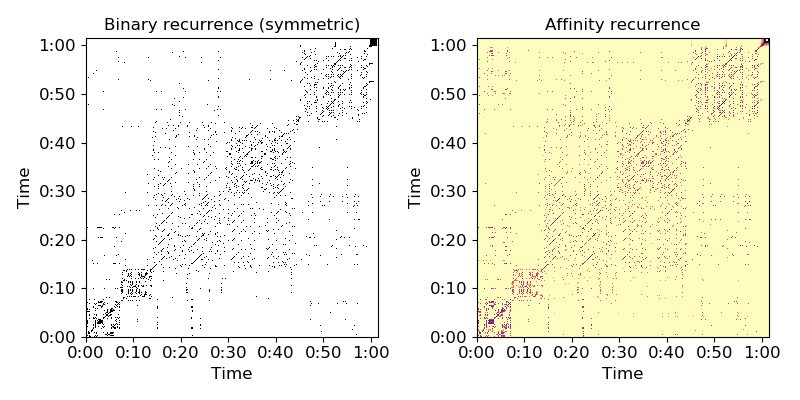
Plot the feature and recurrence matrices

>>> import matplotlib.pyplot as plt
>>> plt.figure(figsize=(8, 4))
>>> plt.subplot(1, 2, 1)
>>> librosa.display.specshow(R, x_axis='time', y_axis='time')
>>> plt.title('Binary recurrence (symmetric)')
>>> plt.subplot(1, 2, 2)
>>> librosa.display.specshow(R_aff, x_axis='time', y_axis='time',
...                          cmap='magma_r')
>>> plt.title('Affinity recurrence')
>>> plt.tight_layout()

(Source code)