librosa.segment.recurrence_to_lag

librosa.segment.recurrence_to_lag(rec, pad=True, axis=-1)

Convert a recurrence matrix into a lag matrix.

lag[i, j] == rec[i+j, j]

Parameters:

rec : np.ndarray, or scipy.sparse.spmatrix [shape=(n, n)]

A (binary) recurrence matrix, as returned by recurrence_matrix

pad : bool

If False, lag matrix is square, which is equivalent to assuming that the signal repeats itself indefinitely.

If True, lag is padded with n zeros, which eliminates the assumption of repetition.

axis : int

The axis to keep as the time axis. The alternate axis will be converted to lag coordinates.

Returns:

lag : np.ndarray

The recurrence matrix in (lag, time) (if axis=1) or (time, lag) (if axis=0) coordinates

Raises:

ParameterError : if rec is non-square

See also

recurrence_matrix, lag_to_recurrence

Examples

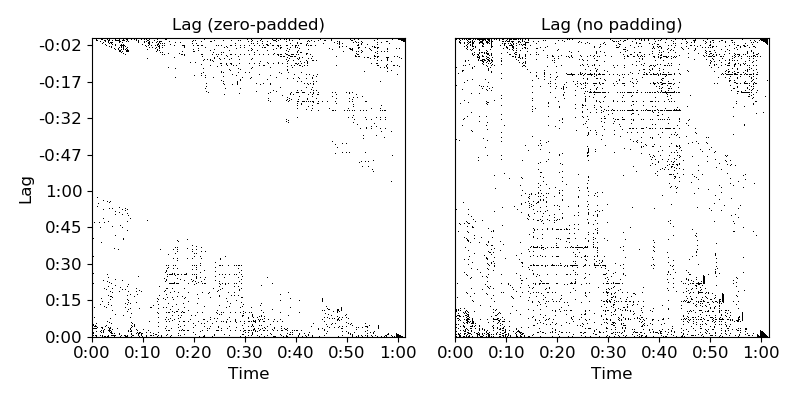
>>> y, sr = librosa.load(librosa.util.example_audio_file())
>>> mfccs = librosa.feature.mfcc(y=y, sr=sr)
>>> recurrence = librosa.segment.recurrence_matrix(mfccs)
>>> lag_pad = librosa.segment.recurrence_to_lag(recurrence, pad=True)
>>> lag_nopad = librosa.segment.recurrence_to_lag(recurrence, pad=False)

>>> import matplotlib.pyplot as plt
>>> plt.figure(figsize=(8, 4))
>>> plt.subplot(1, 2, 1)
>>> librosa.display.specshow(lag_pad, x_axis='time', y_axis='lag')
>>> plt.title('Lag (zero-padded)')
>>> plt.subplot(1, 2, 2)
>>> librosa.display.specshow(lag_nopad, x_axis='time')
>>> plt.title('Lag (no padding)')
>>> plt.tight_layout()

(Source code)