librosa.feature.spectral_rolloff

librosa.feature.spectral_rolloff(y=None, sr=22050, S=None, n_fft=2048, hop_length=512, freq=None, roll_percent=0.85)

Compute roll-off frequency

Parameters:

y : np.ndarray [shape=(n,)] or None

audio time series

sr : number > 0 [scalar]

audio sampling rate of y

S : np.ndarray [shape=(d, t)] or None

(optional) spectrogram magnitude

n_fft : int > 0 [scalar]

FFT window size

hop_length : int > 0 [scalar]

hop length for STFT. See librosa.core.stft for details.

freq : None or np.ndarray [shape=(d,) or shape=(d, t)]

Center frequencies for spectrogram bins. If None, then FFT bin center frequencies are used. Otherwise, it can be a single array of d center frequencies,

Note

freq is assumed to be sorted in increasing order

roll_percent : float [0 < roll_percent < 1]

Roll-off percentage.

Returns:

rolloff : np.ndarray [shape=(1, t)]

roll-off frequency for each frame

Examples

From time-series input

>>> y, sr = librosa.load(librosa.util.example_audio_file())
>>> rolloff = librosa.feature.spectral_rolloff(y=y, sr=sr)
>>> rolloff
array([[ 8376.416,   968.994, ...,  8925.513,  9108.545]])

From spectrogram input

>>> S, phase = librosa.magphase(librosa.stft(y))
>>> librosa.feature.spectral_rolloff(S=S, sr=sr)
array([[ 8376.416,   968.994, ...,  8925.513,  9108.545]])

>>> # With a higher roll percentage:
>>> y, sr = librosa.load(librosa.util.example_audio_file())
>>> librosa.feature.spectral_rolloff(y=y, sr=sr, roll_percent=0.95)
array([[ 10012.939,   3003.882, ...,  10034.473,  10077.539]])

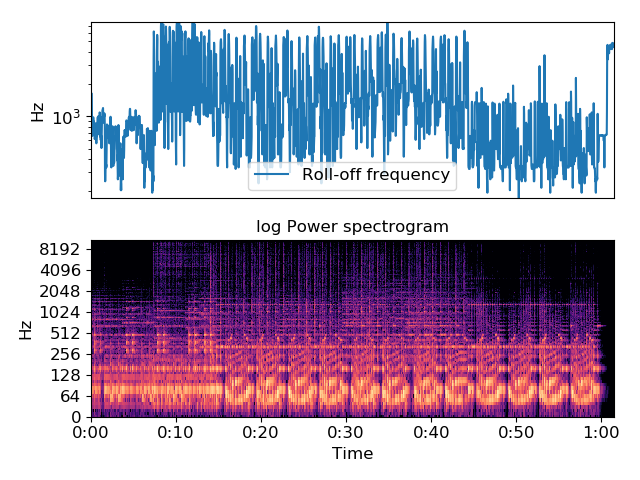
>>> import matplotlib.pyplot as plt
>>> plt.figure()
>>> plt.subplot(2, 1, 1)
>>> plt.semilogy(rolloff.T, label='Roll-off frequency')
>>> plt.ylabel('Hz')
>>> plt.xticks([])
>>> plt.xlim([0, rolloff.shape[-1]])
>>> plt.legend()
>>> plt.subplot(2, 1, 2)
>>> librosa.display.specshow(librosa.amplitude_to_db(S, ref=np.max),
...                          y_axis='log', x_axis='time')
>>> plt.title('log Power spectrogram')
>>> plt.tight_layout()

(Source code)